Derivative

A function of a real variable ${\displaystyle f(x)}$ is differentiable at a point ${\displaystyle a}$ of its domain, if its domain contains an open interval containing ⁠${\displaystyle a}$⁠, and the limit $${\displaystyle L=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}}$$ exists.^[2] This means that, for every positive real number ⁠${\displaystyle \varepsilon }$⁠, there exists a positive real number ${\displaystyle \delta }$ such that, for every ${\displaystyle h}$ such that ${\displaystyle |h|<\delta }$ and ${\displaystyle h\neq 0}$ then ${\displaystyle f(a+h)}$ is defined, and $${\displaystyle \left|L-{\frac {f(a+h)-f(a)}{h}}\right|<\varepsilon ,}$$ where the vertical bars denote the absolute value. This is an example of the (ε, δ)-definition of limit.^[3]

If the function ${\displaystyle f}$ is differentiable at ⁠${\displaystyle a}$⁠, that is if the limit ${\displaystyle L}$ exists, then this limit is called the derivative of ${\displaystyle f}$ at ${\displaystyle a}$. Multiple notations for the derivative exist.^[4] The derivative of ${\displaystyle f}$ at ${\displaystyle a}$ can be denoted ⁠${\displaystyle f'(a)}$⁠, read as "⁠${\displaystyle f}$⁠ prime of ⁠${\displaystyle a}$⁠"; or it can be denoted ⁠${\displaystyle \textstyle {\frac {df}{dx}}(a)}$⁠, read as "the derivative of ${\displaystyle f}$ with respect to ${\displaystyle x}$ at ⁠${\displaystyle a}$⁠" or "⁠${\displaystyle df}$⁠ by (or over) ${\displaystyle dx}$ at ⁠${\displaystyle a}$⁠". See § Notation below. If ${\displaystyle f}$ is a function that has a derivative at every point in its domain, then a function can be defined by mapping every point ${\displaystyle x}$ to the value of the derivative of ${\displaystyle f}$ at ${\displaystyle x}$. This function is written ${\displaystyle f'}$ and is called the derivative function or the derivative of ⁠${\displaystyle f}$⁠. The function ${\displaystyle f}$ sometimes has a derivative at most, but not all, points of its domain. The function whose value at ${\displaystyle a}$ equals ${\displaystyle f'(a)}$ whenever ${\displaystyle f'(a)}$ is defined and elsewhere is undefined is also called the derivative of ⁠${\displaystyle f}$⁠. It is still a function, but its domain may be smaller than the domain of ${\displaystyle f}$.^[5]

For example, let ${\displaystyle f}$ be the squaring function: ${\displaystyle f(x)=x^{2}}$. Then the quotient in the definition of the derivative is^[6] $${\displaystyle {\frac {f(a+h)-f(a)}{h}}={\frac {(a+h)^{2}-a^{2}}{h}}={\frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=2a+h.}$$ The division in the last step is valid as long as ${\displaystyle h\neq 0}$. The closer ${\displaystyle h}$ is to ⁠${\displaystyle 0}$⁠, the closer this expression becomes to the value ${\displaystyle 2a}$. The limit exists, and for every input ${\displaystyle a}$ the limit is ${\displaystyle 2a}$. So, the derivative of the squaring function is the doubling function: ⁠${\displaystyle f'(x)=2x}$⁠.

The ratio in the definition of the derivative is the slope of the line through two points on the graph of the function ⁠${\displaystyle f}$⁠, specifically the points ${\displaystyle (a,f(a))}$ and ${\displaystyle (a+h,f(a+h))}$. As ${\displaystyle h}$ is made smaller, these points grow closer together, and the slope of this line approaches the limiting value, the slope of the tangent to the graph of ${\displaystyle f}$ at ${\displaystyle a}$. In other words, the derivative is the slope of the tangent.^[7]

One way to think of the derivative ${\textstyle {\frac {df}{dx}}(a)}$ is as the ratio of an infinitesimal change in the output of the function ${\displaystyle f}$ to an infinitesimal change in its input.^[8] In order to make this intuition rigorous, a system of rules for manipulating infinitesimal quantities is required.^[9] The system of hyperreal numbers is a way of treating infinite and infinitesimal quantities. The hyperreals are an extension of the real numbers that contain numbers greater than anything of the form ${\displaystyle 1+1+\cdots +1}$ for any finite number of terms. Such numbers are infinite, and their reciprocals are infinitesimals. The application of hyperreal numbers to the foundations of calculus is called nonstandard analysis. This provides a way to define the basic concepts of calculus such as the derivative and integral in terms of infinitesimals, thereby giving a precise meaning to the ${\displaystyle d}$ in the Leibniz notation. Thus, the derivative of ${\displaystyle f(x)}$ becomes $${\displaystyle f'(x)=\operatorname {st} \left({\frac {f(x+dx)-f(x)}{dx}}\right)}$$ for an arbitrary infinitesimal ⁠${\displaystyle dx}$⁠, where ${\displaystyle \operatorname {st} }$ denotes the standard part function, which "rounds off" each finite hyperreal to the nearest real.^[10] Taking the squaring function ${\displaystyle f(x)=x^{2}}$ as an example again, $${\displaystyle {\begin{aligned}f'(x)&=\operatorname {st} \left({\frac {x^{2}+2x\cdot dx+(dx)^{2}-x^{2}}{dx}}\right)\\&=\operatorname {st} \left({\frac {2x\cdot dx+(dx)^{2}}{dx}}\right)\\&=\operatorname {st} \left({\frac {2x\cdot dx}{dx}}+{\frac {(dx)^{2}}{dx}}\right)\\&=\operatorname {st} \left(2x+dx\right)\\&=2x.\end{aligned}}}$$

This function does not have a derivative at the marked point, as the function is not continuous there (specifically, it has a jump discontinuity).

The absolute value function is continuous but fails to be differentiable at x = 0 since the tangent slopes do not approach the same value from the left as they do from the right.

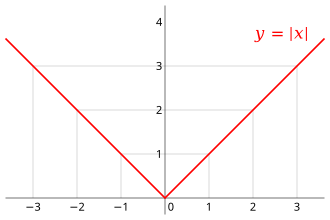
If ${\displaystyle f}$ is differentiable at ⁠${\displaystyle a}$⁠, then ${\displaystyle f}$ must also be continuous at ${\displaystyle a}$.^[11] As an example, choose a point ${\displaystyle a}$ and let ${\displaystyle f}$ be the step function that returns the value 1 for all ${\displaystyle x}$ less than ⁠${\displaystyle a}$⁠, and returns a different value 10 for all ${\displaystyle x}$ greater than or equal to ${\displaystyle a}$. The function ${\displaystyle f}$ cannot have a derivative at ${\displaystyle a}$. If ${\displaystyle h}$ is negative, then ${\displaystyle a+h}$ is on the low part of the step, so the secant line from ${\displaystyle a}$ to ${\displaystyle a+h}$ is very steep; as ${\displaystyle h}$ tends to zero, the slope tends to infinity. If ${\displaystyle h}$ is positive, then ${\displaystyle a+h}$ is on the high part of the step, so the secant line from ${\displaystyle a}$ to ${\displaystyle a+h}$ has slope zero. Consequently, the secant lines do not approach any single slope, so the limit of the difference quotient does not exist. However, even if a function is continuous at a point, it may not be differentiable there. For example, the absolute value function given by ${\displaystyle f(x)=|x|}$ is continuous at ⁠${\displaystyle x=0}$⁠, but it is not differentiable there. If ${\displaystyle h}$ is positive, then the slope of the secant line from 0 to ${\displaystyle h}$ is one; if ${\displaystyle h}$ is negative, then the slope of the secant line from ${\displaystyle 0}$ to ${\displaystyle h}$ is ⁠${\displaystyle -1}$⁠.^[12] This can be seen graphically as a "kink" or a "cusp" in the graph at ${\displaystyle x=0}$. Even a function with a smooth graph is not differentiable at a point where its tangent is vertical: For instance, the function given by ${\displaystyle f(x)=x^{1/3}}$ is not differentiable at ${\displaystyle x=0}$. In summary, a function that has a derivative is continuous, but there are continuous functions that do not have a derivative.^[13]

Most functions that occur in practice have derivatives at all points or almost every point. Early in the history of calculus, many mathematicians assumed that a continuous function was differentiable at most points.^[14] Under mild conditions (for example, if the function is a monotone or a Lipschitz function), this is true. However, in 1872, Weierstrass found the first example of a function that is continuous everywhere but differentiable nowhere. This example is now known as the Weierstrass function.^[15] In 1931, Stefan Banach proved that the set of functions that have a derivative at some point is a meager set in the space of all continuous functions. Informally, this means that hardly any random continuous functions have a derivative at even one point.^[16]

One common way of writing the derivative of a function is Leibniz notation, introduced by Gottfried Wilhelm Leibniz in 1675, which denotes a derivative as the quotient of two differentials, such as ${\displaystyle dy}$ and ⁠${\displaystyle dx}$⁠.^[17] It is still commonly used when the equation ${\displaystyle y=f(x)}$ is viewed as a functional relationship between dependent and independent variables. The first derivative is denoted by ⁠${\displaystyle \textstyle {\frac {dy}{dx}}}$⁠, read as "the derivative of ${\displaystyle y}$ with respect to ⁠${\displaystyle x}$⁠".^[18] This derivative can alternately be treated as the application of a differential operator to a function, ${\textstyle {\frac {dy}{dx}}={\frac {d}{dx}}f(x).}$ Higher derivatives are expressed using the notation ${\textstyle {\frac {d^{n}y}{dx^{n}}}}$ for the ${\displaystyle n}$-th derivative of ${\displaystyle y=f(x)}$. These are abbreviations for multiple applications of the derivative operator; for example, ${\textstyle {\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}{\Bigl (}{\frac {d}{dx}}f(x){\Bigr )}.}$^[19] Unlike some alternatives, Leibniz notation involves explicit specification of the variable for differentiation, in the denominator, which removes ambiguity when working with multiple interrelated quantities. The derivative of a composed function can be expressed using the chain rule: if ${\displaystyle u=g(x)}$ and ${\displaystyle y=f(g(x))}$ then ${\textstyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}.}$^[20]

Another common notation for differentiation is by using the prime mark in the symbol of a function ⁠${\displaystyle f(x)}$⁠. This notation, due to Joseph-Louis Lagrange, is now known as prime notation.^[21] The first derivative is written as ⁠${\displaystyle f'(x)}$⁠, read as "⁠${\displaystyle f}$⁠ prime of ⁠${\displaystyle x}$⁠", or ⁠${\displaystyle y'}$⁠, read as "⁠${\displaystyle y}$⁠ prime".^[22] Similarly, the second and the third derivatives can be written as ${\displaystyle f''}$ and ⁠${\displaystyle f'''}$⁠, respectively.^[23] For denoting the number of higher derivatives beyond this point, some authors use Roman numerals in superscript, whereas others place the number in parentheses, such as ${\displaystyle f^{\mathrm {iv} }}$ or ⁠${\displaystyle f^{(4)}}$⁠.^[24] The latter notation generalizes to yield the notation ${\displaystyle f^{(n)}}$ for the ⁠${\displaystyle n}$⁠th derivative of ⁠${\displaystyle f}$⁠.^[19]

In Newton's notation or the dot notation, a dot is placed over a symbol to represent a time derivative. If ${\displaystyle y}$ is a function of ⁠${\displaystyle t}$⁠, then the first and second derivatives can be written as ${\displaystyle {\dot {y}}}$ and ⁠${\displaystyle {\ddot {y}}}$⁠, respectively. This notation is used exclusively for derivatives with respect to time or arc length. It is typically used in differential equations in physics and differential geometry.^[25] However, the dot notation becomes unmanageable for high-order derivatives (of order 4 or more) and cannot deal with multiple independent variables.

Another notation is D-notation, which represents the differential operator by the symbol ⁠${\displaystyle D}$⁠.^[19] The first derivative is written ${\displaystyle Df(x)}$ and higher derivatives are written with a superscript, so the ${\displaystyle n}$-th derivative is ⁠${\displaystyle D^{n}f(x)}$⁠. This notation is sometimes called Euler notation, although it seems that Leonhard Euler did not use it, and the notation was introduced by Louis François Antoine Arbogast.^[26] To indicate a partial derivative, the variable differentiated by is indicated with a subscript, for example given the function ⁠${\displaystyle u=f(x,y)}$⁠, its partial derivative with respect to ${\displaystyle x}$ can be written ${\displaystyle D_{x}u}$ or ⁠${\displaystyle D_{x}f(x,y)}$⁠. Higher partial derivatives can be indicated by superscripts or multiple subscripts, e.g. ${\textstyle D_{xy}f(x,y)={\frac {\partial }{\partial y}}{\Bigl (}{\frac {\partial }{\partial x}}f(x,y){\Bigr )}}$ and ⁠${\displaystyle \textstyle D_{x}^{2}f(x,y)={\frac {\partial }{\partial x}}{\Bigl (}{\frac {\partial }{\partial x}}f(x,y){\Bigr )}}$⁠.^[27]

In principle, the derivative of a function can be computed from the definition by considering the difference quotient and computing its limit. Once the derivatives of a few simple functions are known, the derivatives of other functions are more easily computed using rules for obtaining derivatives of more complicated functions from simpler ones. This process of finding a derivative is known as differentiation.^[28]

The following are the rules for the derivatives of the most common basic functions. Here, ${\displaystyle a}$ is a real number, and ${\displaystyle e}$ is the base of the natural logarithm, approximately 2.71828.^[29]

• Derivatives of powers:

  ${\displaystyle {\frac {d}{dx}}x^{a}=ax^{a-1}}$

• Functions of exponential, natural logarithm, and logarithm with general base:

  ${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}}$

  ${\displaystyle {\frac {d}{dx}}a^{x}=a^{x}\ln(a)}$, for ${\displaystyle a>0}$

  ${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}}$, for ${\displaystyle x>0}$

  ${\displaystyle {\frac {d}{dx}}\log _{a}(x)={\frac {1}{x\ln(a)}}}$, for ${\displaystyle x,a>0}$

• Trigonometric functions:

  ${\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x)}$

  ${\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x)}$

  ${\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x)}$

• Inverse trigonometric functions:

  ${\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}}}$, for ${\displaystyle -1<x<1}$

  ${\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}}}$, for ${\displaystyle -1<x<1}$

  ${\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}$

The following rules allow deducing derivatives of many functions from the derivatives of the basic functions:^[30]

• Constant rule: if ${\displaystyle f}$ is a constant function, then for all ⁠${\displaystyle x}$⁠,

  ${\displaystyle f'(x)=0.}$

• Sum rule:

  ${\displaystyle (\alpha f+\beta g)'=\alpha f'+\beta g'}$ for all functions ${\displaystyle f}$ and ${\displaystyle g}$ and all real numbers ${\displaystyle \alpha }$ and ⁠${\displaystyle \beta }$⁠.

• Product rule:

  ${\displaystyle (fg)'=f'g+fg'}$ for all functions ${\displaystyle f}$ and ⁠${\displaystyle g}$⁠. As a special case, this rule includes the fact ${\displaystyle (\alpha f)'=\alpha f'}$ whenever ${\displaystyle \alpha }$ is a constant because ${\displaystyle \alpha 'f=0\cdot f=0}$ by the constant rule.

• Quotient rule:

  ${\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}$ for all functions ${\displaystyle f}$ and ${\displaystyle g}$ at all inputs where g ≠ 0.

• Chain rule for composite functions: If ⁠${\displaystyle f(x)=h(g(x))}$⁠, then

  ${\displaystyle f'(x)=h'(g(x))\cdot g'(x).}$

The derivative of the function given by ${\displaystyle f(x)=x^{4}+\sin \left(x^{2}\right)-\ln(x)e^{x}+7}$ is $${\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {d\left(x^{2}\right)}{dx}}\cos \left(x^{2}\right)-{\frac {d\left(\ln {x}\right)}{dx}}e^{x}-\ln(x){\frac {d\left(e^{x}\right)}{dx}}+0\\&=4x^{3}+2x\cos \left(x^{2}\right)-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}$$ Here the second term was computed using the chain rule and the third term using the product rule. The known derivatives of the elementary functions ${\displaystyle x^{2}}$, ${\displaystyle x^{4}}$, ${\displaystyle \sin(x)}$, ${\displaystyle \ln(x)}$, and ${\displaystyle \exp(x)=e^{x}}$, as well as the constant ${\displaystyle 7}$, were also used.

An antiderivative of a function ${\displaystyle f}$ is a function whose derivative is ${\displaystyle f}$. Antiderivatives are not unique: if ${\displaystyle A}$ is an antiderivative of ${\displaystyle f}$, then so is ${\displaystyle A+c}$, where ${\displaystyle c}$ is any constant, because the derivative of a constant is zero.^[31] The fundamental theorem of calculus shows that finding an antiderivative of a function gives a way to compute the areas of shapes bounded by that function. More precisely, the integral of a function over a closed interval is equal to the difference between the values of an antiderivative evaluated at the endpoints of that interval.^[32]

Higher order derivatives are the result of differentiating a function repeatedly. Given that ${\displaystyle f}$ is a differentiable function, the derivative of ${\displaystyle f}$ is the first derivative, denoted as ⁠${\displaystyle f'}$⁠. The derivative of ${\displaystyle f'}$ is the second derivative, denoted as ⁠${\displaystyle f''}$⁠, and the derivative of ${\displaystyle f''}$ is the third derivative, denoted as ⁠${\displaystyle f'''}$⁠. By continuing this process, if it exists, the ⁠${\displaystyle n}$⁠th derivative is the derivative of the ⁠${\displaystyle (n-1)}$⁠th derivative or the derivative of order ⁠${\displaystyle n}$⁠. As has been discussed above, the generalization of derivative of a function ${\displaystyle f}$ may be denoted as ⁠${\displaystyle f^{(n)}}$⁠.^[33] A function that has ${\displaystyle k}$ successive derivatives is called ${\displaystyle k}$ times differentiable. If the ${\displaystyle k}$-th derivative is continuous, then the function is said to be of differentiability class ⁠${\displaystyle C^{k}}$⁠.^[34] A function that has infinitely many derivatives is called infinitely differentiable or smooth.^[35] Any polynomial function is infinitely differentiable; taking derivatives repeatedly will eventually result in a constant function, and all subsequent derivatives of that function are zero.^[36]

One application of higher-order derivatives is in physics. Suppose that a function represents the position of an object at the time. The first derivative of that function is the velocity of an object with respect to time, the second derivative of the function is the acceleration of an object with respect to time,^[28] and the third derivative is the jerk.^[37]

A vector-valued function ${\displaystyle \mathbf {y} }$ of a real variable sends real numbers to vectors in some vector space ${\displaystyle \mathbb {R} ^{n}}$. A vector-valued function can be split up into its coordinate functions ${\displaystyle y_{1}(t),y_{2}(t),\dots ,y_{n}(t)}$, meaning that ${\displaystyle \mathbf {y} =(y_{1}(t),y_{2}(t),\dots ,y_{n}(t))}$. This includes, for example, parametric curves in ${\displaystyle \mathbb {R} ^{2}}$ or ${\displaystyle \mathbb {R} ^{3}}$. The coordinate functions are real-valued functions, so the above definition of derivative applies to them. The derivative of ${\displaystyle \mathbf {y} (t)}$ is defined to be the vector, called the tangent vector, whose coordinates are the derivatives of the coordinate functions. That is,^[38] $${\displaystyle \mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},}$$ if the limit exists. The subtraction in the numerator is the subtraction of vectors, not scalars. If the derivative of ${\displaystyle \mathbf {y} }$ exists for every value of ⁠${\displaystyle t}$⁠, then ${\displaystyle \mathbf {y} '}$ is another vector-valued function.^[38]

Functions can depend upon more than one variable. A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant. Partial derivatives are used in vector calculus and differential geometry. As with ordinary derivatives, multiple notations exist: the partial derivative of a function ${\displaystyle f(x,y,\dots )}$ with respect to the variable ${\displaystyle x}$ is variously denoted by

${\displaystyle f_{x}}$, ${\displaystyle f'_{x}}$, ${\displaystyle \partial _{x}f}$, ${\displaystyle {\frac {\partial }{\partial x}}f}$, or ${\displaystyle {\frac {\partial f}{\partial x}}}$,

among other possibilities.^[39] It can be thought of as the rate of change of the function in the ${\displaystyle x}$-direction.^[40] Here ∂ is a rounded d called the partial derivative symbol. To distinguish it from the letter d, ∂ is sometimes pronounced "der", "del", or "partial" instead of "dee".^[41] For example, let ⁠${\displaystyle f(x,y)=x^{2}+xy+y^{2}}$⁠, then the partial derivative of function ${\displaystyle f}$ with respect to both variables ${\displaystyle x}$ and ${\displaystyle y}$ are, respectively: $${\displaystyle {\frac {\partial f}{\partial x}}=2x+y,\qquad {\frac {\partial f}{\partial y}}=x+2y.}$$ In general, the partial derivative of a function ${\displaystyle f(x_{1},\dots ,x_{n})}$ in the direction ${\displaystyle x_{i}}$ at the point ${\displaystyle (a_{1},\dots ,a_{n})}$ is defined to be:^[42] $${\displaystyle {\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{i},\ldots ,a_{n})}{h}}.}$$

This is fundamental for the study of the functions of several real variables. Let ${\displaystyle f(x_{1},\dots ,x_{n})}$ be such a real-valued function. If all partial derivatives ${\displaystyle f}$ with respect to ${\displaystyle x_{j}}$ are defined at the point ⁠${\displaystyle (a_{1},\dots ,a_{n})}$⁠, these partial derivatives define the vector $${\displaystyle \nabla f(a_{1},\ldots ,a_{n})=\left({\frac {\partial f}{\partial x_{1}}}(a_{1},\ldots ,a_{n}),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a_{1},\ldots ,a_{n})\right),}$$ which is called the gradient of ${\displaystyle f}$ at ${\displaystyle a}$. If ${\displaystyle f}$ is differentiable at every point in some domain, then the gradient is a vector-valued function ${\displaystyle \nabla f}$ that maps the point ${\displaystyle (a_{1},\dots ,a_{n})}$ to the vector ${\displaystyle \nabla f(a_{1},\dots ,a_{n})}$. Consequently, the gradient determines a vector field.^[43]

If ${\displaystyle f}$ is a real-valued function on ⁠${\displaystyle \mathbb {R} ^{n}}$⁠, then the partial derivatives of ${\displaystyle f}$ measure its variation in the direction of the coordinate axes. For example, if ${\displaystyle f}$ is a function of ${\displaystyle x}$ and ⁠${\displaystyle y}$⁠, then its partial derivatives measure the variation in ${\displaystyle f}$ in the ${\displaystyle x}$ and ${\displaystyle y}$ direction. However, they do not directly measure the variation of ${\displaystyle f}$ in any other direction, such as along the diagonal line ⁠${\displaystyle y=x}$⁠. These are measured using directional derivatives. Given a vector ⁠${\displaystyle \mathbf {v} =(v_{1},\ldots ,v_{n})}$⁠, then the directional derivative of ${\displaystyle f}$ in the direction of ${\displaystyle \mathbf {v} }$ at the point ${\displaystyle \mathbf {x} }$ is:^[44] $${\displaystyle D_{\mathbf {v} }{f}(\mathbf {x} )=\lim _{h\rightarrow 0}{\frac {f(\mathbf {x} +h\mathbf {v} )-f(\mathbf {x} )}{h}}.}$$

If all the partial derivatives of ${\displaystyle f}$ exist and are continuous at ⁠${\displaystyle \mathbf {x} }$⁠, then they determine the directional derivative of ${\displaystyle f}$ in the direction ${\displaystyle \mathbf {v} }$ by the formula:^[45] $${\displaystyle D_{\mathbf {v} }{f}(\mathbf {x} )=\sum _{j=1}^{n}v_{j}{\frac {\partial f}{\partial x_{j}}}.}$$

When ${\displaystyle f}$ is a function from an open subset of ${\displaystyle \mathbb {R} ^{n}}$ to ⁠${\displaystyle \mathbb {R} ^{m}}$⁠, then the directional derivative of ${\displaystyle f}$ in a chosen direction is the best linear approximation to ${\displaystyle f}$ at that point and in that direction. However, when ⁠${\displaystyle n>1}$⁠, no single directional derivative can give a complete picture of the behavior of ${\displaystyle f}$. The total derivative gives a complete picture by considering all directions at once. That is, for any vector ${\displaystyle \mathbf {v} }$ starting at ⁠${\displaystyle \mathbf {a} }$⁠, the linear approximation formula holds:^[46] $${\displaystyle f(\mathbf {a} +\mathbf {v} )\approx f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {v} .}$$ Similarly with the single-variable derivative, ${\displaystyle f'(\mathbf {a} )}$ is chosen so that the error in this approximation is as small as possible. The total derivative of ${\displaystyle f}$ at ${\displaystyle \mathbf {a} }$ is the unique linear transformation ${\displaystyle f'(\mathbf {a} )\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$ such that^[46] $${\displaystyle \lim _{\mathbf {h} \to 0}{\frac {\lVert f(\mathbf {a} +\mathbf {h} )-(f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {h} )\rVert }{\lVert \mathbf {h} \rVert }}=0.}$$ Here ${\displaystyle \mathbf {h} }$ is a vector in ⁠${\displaystyle \mathbb {R} ^{n}}$⁠, so the norm in the denominator is the standard length on ${\displaystyle \mathbb {R} ^{n}}$. However, ${\displaystyle f'(\mathbf {a} )\mathbf {h} }$ is a vector in ⁠${\displaystyle \mathbb {R} ^{m}}$⁠, and the norm in the numerator is the standard length on ${\displaystyle \mathbb {R} ^{m}}$.^[46] If ${\displaystyle v}$ is a vector starting at ⁠${\displaystyle a}$⁠, then ${\displaystyle f'(\mathbf {a} )\mathbf {v} }$ is called the pushforward of ${\displaystyle \mathbf {v} }$ by ${\displaystyle f}$.^[47]

If the total derivative exists at ⁠${\displaystyle \mathbf {a} }$⁠, then all the partial derivatives and directional derivatives of ${\displaystyle f}$ exist at ⁠${\displaystyle \mathbf {a} }$⁠, and for all ⁠${\displaystyle \mathbf {v} }$⁠, ${\displaystyle f'(\mathbf {a} )\mathbf {v} }$ is the directional derivative of ${\displaystyle f}$ in the direction ⁠${\displaystyle \mathbf {v} }$⁠. If ${\displaystyle f}$ is written using coordinate functions, so that ⁠${\displaystyle f=(f_{1},f_{2},\dots ,f_{m})}$⁠, then the total derivative can be expressed using the partial derivatives as a matrix. This matrix is called the Jacobian matrix of ${\displaystyle f}$ at ${\displaystyle \mathbf {a} }$:^[48] $${\displaystyle f'(\mathbf {a} )=\operatorname {Jac} _{\mathbf {a} }=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{ij}.}$$

The concept of a derivative can be extended to many other settings. The common thread is that the derivative of a function at a point serves as a linear approximation of the function at that point.

• An important generalization of the derivative concerns complex functions of complex variables, such as functions from (a domain in) the complex numbers ${\displaystyle \mathbb {C} }$ to ⁠${\displaystyle \mathbb {C} }$⁠. The notion of the derivative of such a function is obtained by replacing real variables with complex variables in the definition.^[49] If ${\displaystyle \mathbb {C} }$ is identified with ${\displaystyle \mathbb {R} ^{2}}$ by writing a complex number ${\displaystyle z}$ as ⁠${\displaystyle x+iy}$⁠ then a differentiable function from ${\displaystyle \mathbb {C} }$ to ${\displaystyle \mathbb {C} }$ is certainly differentiable as a function from ${\displaystyle \mathbb {R} ^{2}}$ to ${\displaystyle \mathbb {R} ^{2}}$ (in the sense that its partial derivatives all exist), but the converse is not true in general: the complex derivative only exists if the real derivative is complex linear and this imposes relations between the partial derivatives called the Cauchy–Riemann equations – see holomorphic functions.^[50]
• Another generalization concerns functions between differentiable or smooth manifolds. Intuitively speaking such a manifold ${\displaystyle M}$ is a space that can be approximated near each point ${\displaystyle x}$ by a vector space called its tangent space: the prototypical example is a smooth surface in ⁠${\displaystyle \mathbb {R} ^{3}}$⁠. The derivative (or differential) of a (differentiable) map ${\displaystyle f:M\to N}$ between manifolds, at a point ${\displaystyle x}$ in ⁠${\displaystyle M}$⁠, is then a linear map from the tangent space of ${\displaystyle M}$ at ${\displaystyle x}$ to the tangent space of ${\displaystyle N}$ at ⁠${\displaystyle f(x)}$⁠. The derivative function becomes a map between the tangent bundles of ${\displaystyle M}$ and ⁠${\displaystyle N}$⁠. This definition is used in differential geometry.^[51]
• Differentiation can also be defined for maps between vector space, such as Banach space, in which those generalizations are the Gateaux derivative and the Fréchet derivative.^[52]
• One deficiency of the classical derivative is that very many functions are not differentiable. Nevertheless, there is a way of extending the notion of the derivative so that all continuous functions and many other functions can be differentiated using a concept known as the weak derivative. The idea is to embed the continuous functions in a larger space called the space of distributions and only require that a function is differentiable "on average".^[53]
• Properties of the derivative have inspired the introduction and study of many similar objects in algebra and topology; an example is differential algebra. Here, it consists of the derivation of some topics in abstract algebra, such as rings, ideals, field, and so on.^[54]
• The discrete equivalent of differentiation is finite differences. The study of differential calculus is unified with the calculus of finite differences in time scale calculus.^[55]
• The arithmetic derivative involves the function that is defined for the integers by the prime factorization. This is an analogy with the product rule.^[56]

• Covariant derivative
• Derivation
• Exterior derivative
• Functional derivative
• Lie derivative