Recent from talks
Nothing was collected or created yet.
Mathematics
View on Wikipedia
| Part of a series on | ||
| Mathematics | ||
|---|---|---|
|
|
||
|
| ||
Mathematics is a field of study that discovers and organizes methods, theories, and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics).
Mathematics involves the description and manipulation of abstract objects that consist of either abstractions from nature or—in modern mathematics—purely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to prove properties of objects, a proof consisting of a succession of applications of deductive rules to already established results. These results, called theorems, include previously proved theorems, axioms, and—in case of abstraction from nature—some basic properties that are considered true starting points of the theory under consideration.[1]
Mathematics is essential in the natural sciences, engineering, medicine, finance, computer science, and the social sciences. Although mathematics is extensively used for modeling phenomena, the fundamental truths of mathematics are independent of any scientific experimentation. Some areas of mathematics, such as statistics and game theory, are developed in close correlation with their applications and are often grouped under applied mathematics. Other areas are developed independently from any application (and are therefore called pure mathematics) but often later find practical applications.[2][3]
Historically, the concept of a proof and its associated mathematical rigour first appeared in Greek mathematics, most notably in Euclid's Elements.[4] Since its beginning, mathematics was primarily divided into geometry and arithmetic (the manipulation of natural numbers and fractions), until the 16th and 17th centuries, when algebra[a] and infinitesimal calculus were introduced as new fields. Since then, the interaction between mathematical innovations and scientific discoveries has led to a correlated increase in the development of both.[5] At the end of the 19th century, the foundational crisis of mathematics led to the systematization of the axiomatic method,[6] which heralded a dramatic increase in the number of mathematical areas and their fields of application. The contemporary Mathematics Subject Classification lists more than sixty first-level areas of mathematics.
Areas of mathematics
[edit]Before the Renaissance, mathematics was divided into two main areas: arithmetic, regarding the manipulation of numbers, and geometry, regarding the study of shapes.[7] Some types of pseudoscience, such as numerology and astrology, were not then clearly distinguished from mathematics.[8]
During the Renaissance, two more areas appeared. Mathematical notation led to algebra which, roughly speaking, consists of the study and the manipulation of formulas. Calculus, consisting of the two subfields differential calculus and integral calculus, is the study of continuous functions, which model the typically nonlinear relationships between varying quantities, as represented by variables. This division into four main areas—arithmetic, geometry, algebra, and calculus[9]—endured until the end of the 19th century. Areas such as celestial mechanics and solid mechanics were then studied by mathematicians, but now are considered as belonging to physics.[10] The subject of combinatorics has been studied for much of recorded history, yet did not become a separate branch of mathematics until the seventeenth century.[11]
At the end of the 19th century, the foundational crisis in mathematics and the resulting systematization of the axiomatic method led to an explosion of new areas of mathematics.[12][6] The 2020 Mathematics Subject Classification contains no less than sixty-three first-level areas.[13] Some of these areas correspond to the older division, as is true regarding number theory (the modern name for higher arithmetic) and geometry. Several other first-level areas have "geometry" in their names or are otherwise commonly considered part of geometry. Algebra and calculus do not appear as first-level areas but are respectively split into several first-level areas. Other first-level areas emerged during the 20th century or had not previously been considered as mathematics, such as mathematical logic and foundations.[14]
Number theory
[edit]
Number theory began with the manipulation of numbers, that is, natural numbers and later expanded to integers and rational numbers Number theory was once called arithmetic, but nowadays this term is mostly used for numerical calculations.[15] Number theory dates back to ancient Babylon and probably China. Two prominent early number theorists were Euclid of ancient Greece and Diophantus of Alexandria.[16] The modern study of number theory in its abstract form is largely attributed to Pierre de Fermat and Leonhard Euler. The field came to full fruition with the contributions of Adrien-Marie Legendre and Carl Friedrich Gauss.[17]
Many easily stated number problems have solutions that require sophisticated methods, often from across mathematics. A prominent example is Fermat's Last Theorem. This conjecture was stated in 1637 by Pierre de Fermat, but it was proved only in 1994 by Andrew Wiles, who used tools including scheme theory from algebraic geometry, category theory, and homological algebra.[18] Another example is Goldbach's conjecture, which asserts that every even integer greater than 2 is the sum of two prime numbers. Stated in 1742 by Christian Goldbach, it remains unproven despite considerable effort.[19]
Number theory includes several subareas, including analytic number theory, algebraic number theory, geometry of numbers (method oriented), Diophantine analysis, and transcendence theory (problem oriented).[14]
Geometry
[edit]
Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines, angles and circles, which were developed mainly for the needs of surveying and architecture, but has since blossomed out into many other subfields.[20]
A fundamental innovation was the ancient Greeks' introduction of the concept of proofs, which require that every assertion must be proved. For example, it is not sufficient to verify by measurement that, say, two lengths are equal; their equality must be proven via reasoning from previously accepted results (theorems) and a few basic statements. The basic statements are not subject to proof because they are self-evident (postulates), or are part of the definition of the subject of study (axioms). This principle, foundational for all mathematics, was first elaborated for geometry, and was systematized by Euclid around 300 BC in his book Elements.[21][22]
The resulting Euclidean geometry is the study of shapes and their arrangements constructed from lines, planes and circles in the Euclidean plane (plane geometry) and the three-dimensional Euclidean space.[b][20]
Euclidean geometry was developed without change of methods or scope until the 17th century, when René Descartes introduced what is now called Cartesian coordinates. This constituted a major change of paradigm: Instead of defining real numbers as lengths of line segments (see number line), it allowed the representation of points using their coordinates, which are numbers. Algebra (and later, calculus) can thus be used to solve geometrical problems. Geometry was split into two new subfields: synthetic geometry, which uses purely geometrical methods, and analytic geometry, which uses coordinates systemically.[23]
Analytic geometry allows the study of curves unrelated to circles and lines. Such curves can be defined as the graph of functions, the study of which led to differential geometry. They can also be defined as implicit equations, often polynomial equations (which spawned algebraic geometry). Analytic geometry also makes it possible to consider Euclidean spaces of higher than three dimensions.[20]
In the 19th century, mathematicians discovered non-Euclidean geometries, which do not follow the parallel postulate. By questioning that postulate's truth, this discovery has been viewed as joining Russell's paradox in revealing the foundational crisis of mathematics. This aspect of the crisis was solved by systematizing the axiomatic method, and adopting that the truth of the chosen axioms is not a mathematical problem.[24][6] In turn, the axiomatic method allows for the study of various geometries obtained either by changing the axioms or by considering properties that do not change under specific transformations of the space.[25]
Today's subareas of geometry include:[14]
- Projective geometry, introduced in the 16th century by Girard Desargues, extends Euclidean geometry by adding points at infinity at which parallel lines intersect. This simplifies many aspects of classical geometry by unifying the treatments for intersecting and parallel lines.
- Affine geometry, the study of properties relative to parallelism and independent from the concept of length.
- Differential geometry, the study of curves, surfaces, and their generalizations, which are defined using differentiable functions.
- Manifold theory, the study of shapes that are not necessarily embedded in a larger space.
- Riemannian geometry, the study of distance properties in curved spaces.
- Algebraic geometry, the study of curves, surfaces, and their generalizations, which are defined using polynomials.
- Topology, the study of properties that are kept under continuous deformations.
- Algebraic topology, the use in topology of algebraic methods, mainly homological algebra.
- Discrete geometry, the study of finite configurations in geometry.
- Convex geometry, the study of convex sets, which takes its importance from its applications in optimization.
- Complex geometry, the geometry obtained by replacing real numbers with complex numbers.
Algebra
[edit]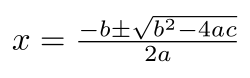

Algebra is the art of manipulating equations and formulas. Diophantus (3rd century) and al-Khwarizmi (9th century) were the two main precursors of algebra.[27][28] Diophantus solved some equations involving unknown natural numbers by deducing new relations until he obtained the solution.[29] Al-Khwarizmi introduced systematic methods for transforming equations, such as moving a term from one side of an equation into the other side.[30] The term algebra is derived from the Arabic word al-jabr meaning 'the reunion of broken parts' that he used for naming one of these methods in the title of his main treatise.[31][32]
Algebra became an area in its own right only with François Viète (1540–1603), who introduced the use of variables for representing unknown or unspecified numbers.[33] Variables allow mathematicians to describe the operations that have to be done on the numbers represented using mathematical formulas.[34]
Until the 19th century, algebra consisted mainly of the study of linear equations (presently linear algebra), and polynomial equations in a single unknown, which were called algebraic equations (a term still in use, although it may be ambiguous). During the 19th century, mathematicians began to use variables to represent things other than numbers (such as matrices, modular integers, and geometric transformations), on which generalizations of arithmetic operations are often valid.[35] The concept of algebraic structure addresses this, consisting of a set whose elements are unspecified, of operations acting on the elements of the set, and rules that these operations must follow. The scope of algebra thus grew to include the study of algebraic structures. This object of algebra was called modern algebra or abstract algebra, as established by the influence and works of Emmy Noether,[36] and popularized by Van der Waerden's book Moderne Algebra.
Some types of algebraic structures have useful and often fundamental properties, in many areas of mathematics. Their study became autonomous parts of algebra, and include:[14]
- group theory
- field theory
- vector spaces, whose study is essentially the same as linear algebra
- ring theory
- commutative algebra, which is the study of commutative rings, includes the study of polynomials, and is a foundational part of algebraic geometry
- homological algebra
- Lie algebra and Lie group theory
- Boolean algebra, which is widely used for the study of the logical structure of computers
The study of types of algebraic structures as mathematical objects is the purpose of universal algebra and category theory.[37] The latter applies to every mathematical structure (not only algebraic ones). At its origin, it was introduced, together with homological algebra for allowing the algebraic study of non-algebraic objects such as topological spaces; this particular area of application is called algebraic topology.[38]
Calculus and analysis
[edit]
Calculus, formerly called infinitesimal calculus, was introduced independently and simultaneously by 17th-century mathematicians Newton and Leibniz.[39] It is fundamentally the study of the relationship between variables that depend continuously on each other. Calculus was expanded in the 18th century by Euler with the introduction of the concept of a function and many other results.[40] Presently, "calculus" refers mainly to the elementary part of this theory, and "analysis" is commonly used for advanced parts.[41]
Analysis is further subdivided into real analysis, where variables represent real numbers, and complex analysis, where variables represent complex numbers. Analysis includes many subareas shared by other areas of mathematics which include:[14]
- Multivariable calculus
- Functional analysis, where variables represent varying functions
- Integration, measure theory and potential theory, all strongly related with probability theory on a continuum
- Ordinary differential equations
- Partial differential equations
- Numerical analysis, mainly devoted to the computation on computers of solutions of ordinary and partial differential equations that arise in many applications
Discrete mathematics
[edit]
Discrete mathematics, broadly speaking, is the study of individual, countable mathematical objects. An example is the set of all integers.[42] Because the objects of study here are discrete, the methods of calculus and mathematical analysis do not directly apply.[c] Algorithms—especially their implementation and computational complexity—play a major role in discrete mathematics.[43]
The four color theorem and optimal sphere packing were two major problems of discrete mathematics solved in the second half of the 20th century.[44] The P versus NP problem, which remains open to this day, is also important for discrete mathematics, since its solution would potentially impact a large number of computationally difficult problems.[45]
Discrete mathematics includes:[14]
- Combinatorics, the art of enumerating mathematical objects that satisfy some given constraints. Originally, these objects were elements or subsets of a given set; this has been extended to various objects, which establishes a strong link between combinatorics and other parts of discrete mathematics. For example, discrete geometry includes counting configurations of geometric shapes.
- Graph theory and hypergraphs
- Coding theory, including error correcting codes and a part of cryptography
- Matroid theory
- Discrete geometry
- Discrete probability distributions
- Game theory (although continuous games are also studied, most common games, such as chess and poker are discrete)
- Discrete optimization, including combinatorial optimization, integer programming, constraint programming
Mathematical logic and set theory
[edit]
The two subjects of mathematical logic and set theory have belonged to mathematics since the end of the 19th century.[46][47] Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to philosophy and was not specifically studied by mathematicians.[48]
Before Cantor's study of infinite sets, mathematicians were reluctant to consider actually infinite collections, and considered infinity to be the result of endless enumeration. Cantor's work offended many mathematicians not only by considering actually infinite sets[49] but by showing that this implies different sizes of infinity, per Cantor's diagonal argument. This led to the controversy over Cantor's set theory.[50] In the same period, various areas of mathematics concluded the former intuitive definitions of the basic mathematical objects were insufficient for ensuring mathematical rigour.[51]
This became the foundational crisis of mathematics.[52] It was eventually solved in mainstream mathematics by systematizing the axiomatic method inside a formalized set theory. Roughly speaking, each mathematical object is defined by the set of all similar objects and the properties that these objects must have.[12] For example, in Peano arithmetic, the natural numbers are defined by "zero is a number", "each number has a unique successor", "each number but zero has a unique predecessor", and some rules of reasoning.[53] This mathematical abstraction from reality is embodied in the modern philosophy of formalism, as founded by David Hilbert around 1910.[54]
The "nature" of the objects defined this way is a philosophical problem that mathematicians leave to philosophers, even if many mathematicians have opinions on this nature, and use their opinion—sometimes called "intuition"—to guide their study and proofs. The approach allows considering "logics" (that is, sets of allowed deducing rules), theorems, proofs, etc. as mathematical objects, and to prove theorems about them. For example, Gödel's incompleteness theorems assert, roughly speaking that, in every consistent formal system that contains the natural numbers, there are theorems that are true (that is provable in a stronger system), but not provable inside the system.[55] This approach to the foundations of mathematics was challenged during the first half of the 20th century by mathematicians led by Brouwer, who promoted intuitionistic logic, which explicitly lacks the law of excluded middle.[56][57]
These problems and debates led to a wide expansion of mathematical logic, with subareas such as model theory (modeling some logical theories inside other theories), proof theory, type theory, computability theory and computational complexity theory.[14] Although these aspects of mathematical logic were introduced before the rise of computers, their use in compiler design, formal verification, program analysis, proof assistants and other aspects of computer science, contributed in turn to the expansion of these logical theories.[58]
Statistics and other decision sciences
[edit]
The field of statistics is a mathematical application that is employed for the collection and processing of data samples, using procedures based on mathematical methods especially probability theory. Statisticians generate data with random sampling or randomized experiments.[60]
Statistical theory studies decision problems such as minimizing the risk (expected loss) of a statistical action, such as using a procedure in, for example, parameter estimation, hypothesis testing, and selecting the best. In these traditional areas of mathematical statistics, a statistical-decision problem is formulated by minimizing an objective function, like expected loss or cost, under specific constraints. For example, designing a survey often involves minimizing the cost of estimating a population mean with a given level of confidence.[61] Because of its use of optimization, the mathematical theory of statistics overlaps with other decision sciences, such as operations research, control theory, and mathematical economics.[62]
Computational mathematics
[edit]Computational mathematics is the study of mathematical problems that are typically too large for human, numerical capacity.[63][64] Numerical analysis studies methods for problems in analysis using functional analysis and approximation theory; numerical analysis broadly includes the study of approximation and discretization with special focus on rounding errors.[65] Numerical analysis and, more broadly, scientific computing also study non-analytic topics of mathematical science, especially algorithmic-matrix-and-graph theory. Other areas of computational mathematics include computer algebra and symbolic computation.
History
[edit]Etymology
[edit]The word mathematics comes from the Ancient Greek word máthēma (μάθημα), meaning 'something learned, knowledge, mathematics', and the derived expression mathēmatikḗ tékhnē (μαθηματικὴ τέχνη), meaning 'mathematical science'. It entered the English language during the Late Middle English period through French and Latin.[66]
Similarly, one of the two main schools of thought in Pythagoreanism was known as the mathēmatikoi (μαθηματικοί)—which at the time meant "learners" rather than "mathematicians" in the modern sense. The Pythagoreans were likely the first to constrain the use of the word to just the study of arithmetic and geometry. By the time of Aristotle (384–322 BC) this meaning was fully established.[67]
In Latin and English, until around 1700, the term mathematics more commonly meant "astrology" (or sometimes "astronomy") rather than "mathematics"; the meaning gradually changed to its present one from about 1500 to 1800. This change has resulted in several mistranslations: For example, Saint Augustine's warning that Christians should beware of mathematici, meaning "astrologers", is sometimes mistranslated as a condemnation of mathematicians.[68]
The apparent plural form in English goes back to the Latin neuter plural mathematica (Cicero), based on the Greek plural ta mathēmatiká (τὰ μαθηματικά) and means roughly "all things mathematical", although it is plausible that English borrowed only the adjective mathematic(al) and formed the noun mathematics anew, after the pattern of physics and metaphysics, inherited from Greek.[69] In English, the noun mathematics takes a singular verb. It is often shortened to maths[70] or, in North America, math.[71]
Ancient
[edit]
In addition to recognizing how to count physical objects, prehistoric peoples may have also known how to count abstract quantities, like time—days, seasons, or years.[72][73] Evidence for more complex mathematics does not appear until around 3000 BC, when the Babylonians and Egyptians began using arithmetic, algebra, and geometry for taxation and other financial calculations, for building and construction, and for astronomy.[74] The oldest mathematical texts from Mesopotamia and Egypt are from 2000 to 1800 BC.[75] Many early texts mention Pythagorean triples and so, by inference, the Pythagorean theorem seems to be the most ancient and widespread mathematical concept after basic arithmetic and geometry. It is in Babylonian mathematics that elementary arithmetic (addition, subtraction, multiplication, and division) first appear in the archaeological record. The Babylonians also possessed a place-value system and used a sexagesimal numeral system which is still in use today for measuring angles and time.[76]
In the 6th century BC, Greek mathematics began to emerge as a distinct discipline and some Ancient Greeks such as the Pythagoreans appeared to have considered it a subject in its own right.[77] Around 300 BC, Euclid organized mathematical knowledge by way of postulates and first principles, which evolved into the axiomatic method that is used in mathematics today, consisting of definition, axiom, theorem, and proof.[78] His book, Elements, is widely considered the most successful and influential textbook of all time.[79] The greatest mathematician of antiquity is often held to be Archimedes (c. 287 – c. 212 BC) of Syracuse.[80] He developed formulas for calculating the surface area and volume of solids of revolution and used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, in a manner not too dissimilar from modern calculus.[81] Other notable achievements of Greek mathematics are conic sections (Apollonius of Perga, 3rd century BC),[82] trigonometry (Hipparchus of Nicaea, 2nd century BC),[83] and the beginnings of algebra (Diophantus, 3rd century AD).[84]

The Hindu–Arabic numeral system and the rules for the use of its operations, in use throughout the world today, evolved over the course of the first millennium AD in India and were transmitted to the Western world via Islamic mathematics.[85] Other notable developments of Indian mathematics include the modern definition and approximation of sine and cosine, and an early form of infinite series.[86][87]
Medieval and later
[edit]
During the Golden Age of Islam, especially during the 9th and 10th centuries, mathematics saw many important innovations building on Greek mathematics. The most notable achievement of Islamic mathematics was the development of algebra. Other achievements of the Islamic period include advances in spherical trigonometry and the addition of the decimal point to the Arabic numeral system.[88] Many notable mathematicians from this period were Persian, such as Al-Khwarizmi, Omar Khayyam and Sharaf al-Dīn al-Ṭūsī.[89] The Greek and Arabic mathematical texts were in turn translated to Latin during the Middle Ages and made available in Europe.[90]
During the early modern period, mathematics began to develop at an accelerating pace in Western Europe, with innovations that revolutionized mathematics, such as the introduction of variables and symbolic notation by François Viète (1540–1603), the introduction of logarithms by John Napier in 1614, which greatly simplified numerical calculations, especially for astronomy and marine navigation, the introduction of coordinates by René Descartes (1596–1650) for reducing geometry to algebra, and the development of calculus by Isaac Newton (1643–1727) and Gottfried Leibniz (1646–1716). Leonhard Euler (1707–1783), the most notable mathematician of the 18th century, unified these innovations into a single corpus with a standardized terminology, and completed them with the discovery and the proof of numerous theorems.[91]

Perhaps the foremost mathematician of the 19th century was the German mathematician Carl Gauss, who made numerous contributions to fields such as algebra, analysis, differential geometry, matrix theory, number theory, and statistics.[92] In the early 20th century, Kurt Gödel transformed mathematics by publishing his incompleteness theorems, which show in part that any consistent axiomatic system—if powerful enough to describe arithmetic—will contain true propositions that cannot be proved.[55]
Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries continue to be made to this very day. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews (MR) database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."[93]
Symbolic notation and terminology
[edit]
Mathematical notation is widely used in science and engineering for representing complex concepts and properties in a concise, unambiguous, and accurate way. This notation consists of symbols used for representing operations, unspecified numbers, relations and any other mathematical objects, and then assembling them into expressions and formulas.[94] More precisely, numbers and other mathematical objects are represented by symbols called variables, which are generally Latin or Greek letters, and often include subscripts. Operation and relations are generally represented by specific symbols or glyphs,[95] such as + (plus), × (multiplication), (integral), = (equal), and < (less than).[96] All these symbols are generally grouped according to specific rules to form expressions and formulas.[97] Normally, expressions and formulas do not appear alone, but are included in sentences of the current language, where expressions play the role of noun phrases and formulas play the role of clauses.
Mathematics has developed a rich terminology covering a broad range of fields that study the properties of various abstract, idealized objects and how they interact. It is based on rigorous definitions that provide a standard foundation for communication. An axiom or postulate is a mathematical statement that is taken to be true without need of proof. If a mathematical statement has yet to be proven (or disproven), it is termed a conjecture. Through a series of rigorous arguments employing deductive reasoning, a statement that is proven to be true becomes a theorem. A specialized theorem that is mainly used to prove another theorem is called a lemma. A proven instance that forms part of a more general finding is termed a corollary.[98]
Numerous technical terms used in mathematics are neologisms, such as polynomial and homeomorphism.[99] Other technical terms are words of the common language that are used in an accurate meaning that may differ slightly from their common meaning. For example, in mathematics, "or" means "one, the other or both", while, in common language, it is either ambiguous or means "one or the other but not both" (in mathematics, the latter is called "exclusive or"). Finally, many mathematical terms are common words that are used with a completely different meaning.[100] This may lead to sentences that are correct and true mathematical assertions, but appear to be nonsense to people who do not have the required background. For example, "every free module is flat" and "a field is always a ring".
Relationship with sciences
[edit]Mathematics is used in most sciences for modeling phenomena, which then allows predictions to be made from experimental laws.[101] The independence of mathematical truth from any experimentation implies that the accuracy of such predictions depends only on the adequacy of the model.[102] Inaccurate predictions, rather than being caused by invalid mathematical concepts, imply the need to change the mathematical model used.[103] For example, the perihelion precession of Mercury could only be explained after the emergence of Einstein's general relativity, which replaced Newton's law of gravitation as a better mathematical model.[104]
There is still a philosophical debate whether mathematics is a science. However, in practice, mathematicians are typically grouped with scientists, and mathematics shares much in common with the physical sciences. Like them, it is falsifiable, which means in mathematics that, if a result or a theory is wrong, this can be proved by providing a counterexample. Similarly as in science, theories and results (theorems) are often obtained from experimentation.[105] In mathematics, the experimentation may consist of computation on selected examples or of the study of figures or other representations of mathematical objects (often mind representations without physical support). For example, when asked how he came about his theorems, Gauss once replied "durch planmässiges Tattonieren" (through systematic experimentation).[106] However, some authors emphasize that mathematics differs from the modern notion of science by not relying on empirical evidence.[107][108][109][110]
Pure and applied mathematics
[edit]Until the 19th century, the development of mathematics in the West was mainly motivated by the needs of technology and science, and there was no clear distinction between pure and applied mathematics.[111] For example, the natural numbers and arithmetic were introduced for the need of counting, and geometry was motivated by surveying, architecture, and astronomy. Later, Isaac Newton introduced infinitesimal calculus for explaining the movement of the planets with his law of gravitation. Moreover, most mathematicians were also scientists, and many scientists were also mathematicians.[112] However, a notable exception occurred with the tradition of pure mathematics in Ancient Greece.[113] The problem of integer factorization, for example, which goes back to Euclid in 300 BC, had no practical application before its use in the RSA cryptosystem, now widely used for the security of computer networks.[114]
In the 19th century, mathematicians such as Karl Weierstrass and Richard Dedekind increasingly focused their research on internal problems, that is, pure mathematics.[111][115] This led to split mathematics into pure mathematics and applied mathematics, the latter being often considered as having a lower value among mathematical purists. However, the lines between the two are frequently blurred.[116]
The aftermath of World War II led to a surge in the development of applied mathematics in the US and elsewhere.[117][118] Many of the theories developed for applications were found interesting from the point of view of pure mathematics, and many results of pure mathematics were shown to have applications outside mathematics; in turn, the study of these applications may give new insights on the "pure theory".[119][120]
An example of the first case is the theory of distributions, introduced by Laurent Schwartz for validating computations done in quantum mechanics, which became immediately an important tool of (pure) mathematical analysis.[121] An example of the second case is the decidability of the first-order theory of the real numbers, a problem of pure mathematics that was proved true by Alfred Tarski, with an algorithm that is impossible to implement because of a computational complexity that is much too high.[122] For getting an algorithm that can be implemented and can solve systems of polynomial equations and inequalities, George Collins introduced the cylindrical algebraic decomposition that became a fundamental tool in real algebraic geometry.[123]
In the present day, the distinction between pure and applied mathematics is more a question of personal research aim of mathematicians than a division of mathematics into broad areas.[124][125] The Mathematics Subject Classification has a section for "general applied mathematics" but does not mention "pure mathematics".[14] However, these terms are still used in names of some university departments, such as at the Faculty of Mathematics at the University of Cambridge.
Unreasonable effectiveness
[edit]The unreasonable effectiveness of mathematics is a phenomenon that was named and first made explicit by physicist Eugene Wigner.[3] It is the fact that many mathematical theories (even the "purest") have applications outside their initial object. These applications may be completely outside their initial area of mathematics, and may concern physical phenomena that were completely unknown when the mathematical theory was introduced.[126] Examples of unexpected applications of mathematical theories can be found in many areas of mathematics.
A notable example is the prime factorization of natural numbers that was discovered more than 2,000 years before its common use for secure internet communications through the RSA cryptosystem.[127] A second historical example is the theory of ellipses. They were studied by the ancient Greek mathematicians as conic sections (that is, intersections of cones with planes). It was almost 2,000 years later that Johannes Kepler discovered that the trajectories of the planets are ellipses.[128]
In the 19th century, the internal development of geometry (pure mathematics) led to definition and study of non-Euclidean geometries, spaces of dimension higher than three and manifolds. At this time, these concepts seemed totally disconnected from the physical reality, but at the beginning of the 20th century, Albert Einstein developed the theory of relativity that uses fundamentally these concepts. In particular, spacetime of special relativity is a non-Euclidean space of dimension four, and spacetime of general relativity is a (curved) manifold of dimension four.[129][130]
A striking aspect of the interaction between mathematics and physics is when mathematics drives research in physics. This is illustrated by the discoveries of the positron and the baryon In both cases, the equations of the theories had unexplained solutions, which led to conjecture of the existence of an unknown particle, and the search for these particles. In both cases, these particles were discovered a few years later by specific experiments.[131][132][133]
Specific sciences
[edit]Physics
[edit]
Mathematics and physics have influenced each other over their modern history. Modern physics uses mathematics abundantly,[134] and is also considered to be the motivation of major mathematical developments.[135]
Computing
[edit]Computing is closely related to mathematics in several ways.[136] Theoretical computer science is considered to be mathematical in nature.[137] Communication technologies apply branches of mathematics that may be very old (e.g., arithmetic), especially with respect to transmission security, in cryptography and coding theory. Discrete mathematics is useful in many areas of computer science, such as complexity theory, information theory, and graph theory.[138] In 1998, the Kepler conjecture on sphere packing seemed to also be partially proven by computer.[139]
Biology and chemistry
[edit]
Biology uses probability extensively in fields such as ecology or neurobiology.[140] Most discussion of probability centers on the concept of evolutionary fitness.[140] Ecology heavily uses modeling to simulate population dynamics,[140][141] study ecosystems such as the predator-prey model, measure pollution diffusion,[142] or to assess climate change.[143] The dynamics of a population can be modeled by coupled differential equations, such as the Lotka–Volterra equations.[144]
Statistical hypothesis testing, is run on data from clinical trials to determine whether a new treatment works.[145] Since the start of the 20th century, chemistry has used computing to model molecules in three dimensions.[146]
Earth sciences
[edit]Structural geology and climatology use probabilistic models to predict the risk of natural catastrophes.[147] Similarly, meteorology, oceanography, and planetology also use mathematics due to their heavy use of models.[148][149][150]
Social sciences
[edit]Areas of mathematics used in the social sciences include probability/statistics and differential equations. These are used in linguistics, economics, sociology,[151] and psychology.[152]
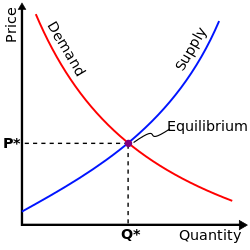
Often the fundamental postulate of mathematical economics is that of the rational individual actor – Homo economicus (lit. 'economic man').[153] In this model, the individual seeks to maximize their self-interest,[153] and always makes optimal choices using perfect information.[154] This atomistic view of economics allows it to relatively easily mathematize its thinking, because individual calculations are transposed into mathematical calculations. Such mathematical modeling allows one to probe economic mechanisms. Some reject or criticise the concept of Homo economicus. Economists note that real people have limited information, make poor choices, and care about fairness and altruism, not just personal gain.[155]
Without mathematical modeling, it is hard to go beyond statistical observations or untestable speculation. Mathematical modeling allows economists to create structured frameworks to test hypotheses and analyze complex interactions. Models provide clarity and precision, enabling the translation of theoretical concepts into quantifiable predictions that can be tested against real-world data.[156]
At the start of the 20th century, there was a development to express historical movements in formulas. In 1922, Nikolai Kondratiev discerned the ~50-year-long Kondratiev cycle, which explains phases of economic growth or crisis.[157] Towards the end of the 19th century, mathematicians extended their analysis into geopolitics.[158] Peter Turchin developed cliodynamics in the 1990s.[159]
Mathematization of the social sciences is not without risk. In the controversial book Fashionable Nonsense (1997), Sokal and Bricmont denounced the unfounded or abusive use of scientific terminology, particularly from mathematics or physics, in the social sciences.[160] The study of complex systems (evolution of unemployment, business capital, demographic evolution of a population, etc.) uses mathematical knowledge. However, the choice of counting criteria, particularly for unemployment, or of models, can be subject to controversy.[161][162]
Philosophy
[edit]Reality
[edit]The connection between mathematics and material reality has led to philosophical debates since at least the time of Pythagoras. The ancient philosopher Plato argued that abstractions that reflect material reality have themselves a reality that exists outside space and time. As a result, the philosophical view that mathematical objects somehow exist on their own in abstraction is often referred to as Platonism. Independently of their possible philosophical opinions, modern mathematicians may be generally considered as Platonists, since they think of and talk of their objects of study as real objects.[163]
Armand Borel summarized this view of mathematics reality as follows, and provided quotations of G. H. Hardy, Charles Hermite, Henri Poincaré and Albert Einstein that support his views.[131]
Something becomes objective (as opposed to "subjective") as soon as we are convinced that it exists in the minds of others in the same form as it does in ours and that we can think about it and discuss it together.[164] Because the language of mathematics is so precise, it is ideally suited to defining concepts for which such a consensus exists. In my opinion, that is sufficient to provide us with a feeling of an objective existence, of a reality of mathematics ...
Nevertheless, Platonism and the concurrent views on abstraction do not explain the unreasonable effectiveness of mathematics (as Platonism assumes mathematics exists independently, but does not explain why it matches reality).[165]
Proposed definitions
[edit]There is no general consensus about the definition of mathematics or its epistemological status—that is, its place inside knowledge. A great many professional mathematicians take no interest in a definition of mathematics, or consider it undefinable. There is not even consensus on whether mathematics is an art or a science. Some just say, "mathematics is what mathematicians do".[166][167] A common approach is to define mathematics by its object of study.[168][169][170][171]
Aristotle defined mathematics as "the science of quantity" and this definition prevailed until the 18th century. However, Aristotle also noted a focus on quantity alone may not distinguish mathematics from sciences like physics; in his view, abstraction and studying quantity as a property "separable in thought" from real instances set mathematics apart.[172] In the 19th century, when mathematicians began to address topics—such as infinite sets—which have no clear-cut relation to physical reality, a variety of new definitions were given.[173] With the large number of new areas of mathematics that have appeared since the beginning of the 20th century, defining mathematics by its object of study has become increasingly difficult.[174] For example, in lieu of a definition, Saunders Mac Lane in Mathematics, form and function summarizes the basics of several areas of mathematics, emphasizing their inter-connectedness, and observes:[175]
the development of Mathematics provides a tightly connected network of formal rules, concepts, and systems. Nodes of this network are closely bound to procedures useful in human activities and to questions arising in science. The transition from activities to the formal Mathematical systems is guided by a variety of general insights and ideas.
Another approach for defining mathematics is to use its methods. For example, an area of study is often qualified as mathematics as soon as one can prove theorems—assertions whose validity relies on a proof, that is, a purely logical deduction.[d][176][failed verification]
Rigor
[edit]Mathematical reasoning requires rigor. This means that the definitions must be absolutely unambiguous and the proofs must be reducible to a succession of applications of inference rules,[e] without any use of empirical evidence and intuition.[f][177] Rigorous reasoning is not specific to mathematics, but, in mathematics, the standard of rigor is much higher than elsewhere. Despite mathematics' concision, rigorous proofs can require hundreds of pages to express, such as the 255-page Feit–Thompson theorem.[g] The emergence of computer-assisted proofs has allowed proof lengths to further expand.[h][178] The result of this trend is a philosophy of the quasi-empiricist proof that can not be considered infallible, but has a probability attached to it.[6]
The concept of rigor in mathematics dates back to ancient Greece, where their society encouraged logical, deductive reasoning. However, this rigorous approach would tend to discourage exploration of new approaches, such as irrational numbers and concepts of infinity. The method of demonstrating rigorous proof was enhanced in the sixteenth century through the use of symbolic notation. In the 18th century, social transition led to mathematicians earning their keep through teaching, which led to more careful thinking about the underlying concepts of mathematics. This produced more rigorous approaches, while transitioning from geometric methods to algebraic and then arithmetic proofs.[6]
At the end of the 19th century, it appeared that the definitions of the basic concepts of mathematics were not accurate enough for avoiding paradoxes (non-Euclidean geometries and Weierstrass function) and contradictions (Russell's paradox). This was solved by the inclusion of axioms with the apodictic inference rules of mathematical theories; the re-introduction of axiomatic method pioneered by the ancient Greeks.[6] It results that "rigor" is no more a relevant concept in mathematics, as a proof is either correct or erroneous, and a "rigorous proof" is simply a pleonasm. Where a special concept of rigor comes into play is in the socialized aspects of a proof, wherein it may be demonstrably refuted by other mathematicians. After a proof has been accepted for many years or even decades, it can then be considered as reliable.[179]
Nevertheless, the concept of "rigor" may remain useful for teaching to beginners what is a mathematical proof.[180]
Training and practice
[edit]Education
[edit]Mathematics has a remarkable ability to cross cultural boundaries and time periods. As a human activity, the practice of mathematics has a social side, which includes education, careers, recognition, popularization, and so on. In education, mathematics is a core part of the curriculum and forms an important element of the STEM academic disciplines. Prominent careers for professional mathematicians include mathematics teacher or professor, statistician, actuary, financial analyst, economist, accountant, commodity trader, or computer consultant.[181]
Archaeological evidence shows that instruction in mathematics occurred as early as the second millennium BCE in ancient Babylonia.[182] Comparable evidence has been unearthed for scribal mathematics training in the ancient Near East and then for the Greco-Roman world starting around 300 BCE.[183] The oldest known mathematics textbook is the Rhind papyrus, dated from c. 1650 BCE in Egypt.[184] Due to a scarcity of books, mathematical teachings in ancient India were communicated using memorized oral tradition since the Vedic period (c. 1500 – c. 500 BCE).[185] In Imperial China during the Tang dynasty (618–907 CE), a mathematics curriculum was adopted for the civil service exam to join the state bureaucracy.[186]
Following the Dark Ages, mathematics education in Europe was provided by religious schools as part of the Quadrivium. Formal instruction in pedagogy began with Jesuit schools in the 16th and 17th century. Most mathematical curricula remained at a basic and practical level until the nineteenth century, when it began to flourish in France and Germany. The oldest journal addressing instruction in mathematics was L'Enseignement Mathématique, which began publication in 1899.[187] The Western advancements in science and technology led to the establishment of centralized education systems in many nation-states, with mathematics as a core component—initially for its military applications.[188] While the content of courses varies, in the present day nearly all countries teach mathematics to students for significant amounts of time.[189]
During school, mathematical capabilities and positive expectations have a strong association with career interest in the field. Extrinsic factors such as feedback motivation by teachers, parents, and peer groups can influence the level of interest in mathematics.[190] Some students studying mathematics may develop an apprehension or fear about their performance in the subject. This is known as mathematical anxiety, and is considered the most prominent of the disorders impacting academic performance. Mathematical anxiety can develop due to various factors such as parental and teacher attitudes, social stereotypes, and personal traits. Help to counteract the anxiety can come from changes in instructional approaches, by interactions with parents and teachers, and by tailored treatments for the individual.[191]
Psychology (aesthetic, creativity and intuition)
[edit]The validity of a mathematical theorem relies only on the rigor of its proof, which could theoretically be done automatically by a computer program. This does not mean that there is no place for creativity in a mathematical work. On the contrary, many important mathematical results (theorems) are solutions of problems that other mathematicians failed to solve, and the invention of a way for solving them may be a fundamental way of the solving process.[192][193] An extreme example is Apery's theorem: Roger Apery provided only the ideas for a proof, and the formal proof was given only several months later by three other mathematicians.[194]
Creativity and rigor are not the only psychological aspects of the activity of mathematicians. Some mathematicians can see their activity as a game, more specifically as solving puzzles.[195] This aspect of mathematical activity is emphasized in recreational mathematics.
Mathematicians can find an aesthetic value to mathematics. Like beauty, it is hard to define, it is commonly related to elegance, which involves qualities like simplicity, symmetry, completeness, and generality. G. H. Hardy in A Mathematician's Apology expressed the belief that the aesthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. He also identified other criteria such as significance, unexpectedness, and inevitability, which contribute to mathematical aesthetics.[196] Paul Erdős expressed this sentiment more ironically by speaking of "The Book", a supposed divine collection of the most beautiful proofs. The 1998 book Proofs from THE BOOK, inspired by Erdős, is a collection of particularly succinct and revelatory mathematical arguments. Some examples of particularly elegant results included are Euclid's proof that there are infinitely many prime numbers and the fast Fourier transform for harmonic analysis.[197]
Some feel that to consider mathematics a science is to downplay its artistry and history in the seven traditional liberal arts.[198] One way this difference of viewpoint plays out is in the philosophical debate as to whether mathematical results are created (as in art) or discovered (as in science).[131] The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.
Cultural impact
[edit]Artistic expression
[edit]Notes that sound well together to a Western ear are sounds whose fundamental frequencies of vibration are in simple ratios. For example, an octave doubles the frequency and a perfect fifth multiplies it by .[199][200]
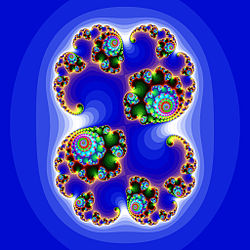
Humans, as well as some other animals, find symmetric patterns to be more beautiful.[201] Mathematically, the symmetries of an object form a group known as the symmetry group.[202] For example, the group underlying mirror symmetry is the cyclic group of two elements, . A Rorschach test is a figure invariant by this symmetry,[203] as are butterfly and animal bodies more generally (at least on the surface).[204] Waves on the sea surface possess translation symmetry: moving one's viewpoint by the distance between wave crests does not change one's view of the sea.[205] Fractals possess self-similarity.[206][207]
Popularization
[edit]Popular mathematics is the act of presenting mathematics without technical terms.[208] Presenting mathematics may be hard since the general public suffers from mathematical anxiety and mathematical objects are highly abstract.[209] However, popular mathematics writing can overcome this by using applications or cultural links.[210] Despite this, mathematics is rarely the topic of popularization in printed or televised media.
Awards and prize problems
[edit]
The most prestigious award in mathematics is the Fields Medal,[211][212] established by Canadian John Charles Fields in 1936 and awarded every four years (except around World War II) to up to four individuals.[213][214] It is considered the mathematical equivalent of the Nobel Prize.[214]
Other prestigious mathematics awards include:[215]
- The Abel Prize, instituted in 2002[216] and first awarded in 2003[217]
- The Chern Medal for lifetime achievement, introduced in 2009[218] and first awarded in 2010[219]
- The AMS Leroy P. Steele Prize, awarded since 1970[220]
- The Wolf Prize in Mathematics, also for lifetime achievement,[221] instituted in 1978[222]
A famous list of 23 open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert.[223] This list has achieved great celebrity among mathematicians,[224] and at least thirteen of the problems (depending how some are interpreted) have been solved.[223]
A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Only one of them, the Riemann hypothesis, duplicates one of Hilbert's problems. A solution to any of these problems carries a 1 million dollar reward.[225] To date, only one of these problems, the Poincaré conjecture, has been solved, by the Russian mathematician Grigori Perelman.[226]
See also
[edit]- Law (mathematics)
- List of mathematical jargon
- Lists of mathematicians
- Lists of mathematics topics
- Mathematical constant
- Mathematical sciences
- Mathematics and art
- Mathematics education
- Philosophy of mathematics
- Relationship between mathematics and physics
- Science, technology, engineering, and mathematics
Notes
[edit]- ^ Here, algebra is taken in its modern sense, which is, roughly speaking, the art of manipulating formulas.
- ^ This includes conic sections, which are intersections of circular cylinders and planes.
- ^ However, some advanced methods of analysis are sometimes used; for example, methods of complex analysis applied to generating series.
- ^ For example, logic belongs to philosophy since Aristotle. Circa the end of the 19th century, the foundational crisis of mathematics implied developments of logic that are specific to mathematics. This allowed eventually the proof of theorems such as Gödel's theorems. Since then, mathematical logic is commonly considered as an area of mathematics.
- ^ This does not mean to make explicit all inference rules that are used. On the contrary, this is generally impossible, without computers and proof assistants. Even with this modern technology, it may take years of human work for writing down a completely detailed proof.
- ^ This does not mean that empirical evidence and intuition are not needed for choosing the theorems to be proved and to prove them.
- ^ This is the length of the original paper that does not contain the proofs of some previously published auxiliary results. The book devoted to the complete proof has more than 1,000 pages.
- ^ For considering as reliable a large computation occurring in a proof, one generally requires two computations using independent software
References
[edit]Citations
[edit]- ^ Hipólito, Inês Viegas (August 9–15, 2015). "Abstract Cognition and the Nature of Mathematical Proof". In Kanzian, Christian; Mitterer, Josef; Neges, Katharina (eds.). Realismus – Relativismus – Konstruktivismus: Beiträge des 38. Internationalen Wittgenstein Symposiums [Realism – Relativism – Constructivism: Contributions of the 38th International Wittgenstein Symposium] (PDF) (in German and English). Vol. 23. Kirchberg am Wechsel, Austria: Austrian Ludwig Wittgenstein Society. pp. 132–134. ISSN 1022-3398. OCLC 236026294. Archived (PDF) from the original on November 7, 2022. Retrieved January 17, 2024. (at ResearchGate
 Archived November 5, 2022, at the Wayback Machine)
Archived November 5, 2022, at the Wayback Machine)
- ^ Peterson 1988, p. 12.
- ^ a b Wigner, Eugene (1960). "The Unreasonable Effectiveness of Mathematics in the Natural Sciences". Communications on Pure and Applied Mathematics. 13 (1): 1–14. Bibcode:1960CPAM...13....1W. doi:10.1002/cpa.3160130102. S2CID 6112252. Archived from the original on February 28, 2011.
- ^ Wise, David. "Eudoxus' Influence on Euclid's Elements with a close look at The Method of Exhaustion". The University of Georgia. Archived from the original on June 1, 2019. Retrieved January 18, 2024.
- ^ Alexander, Amir (September 2011). "The Skeleton in the Closet: Should Historians of Science Care about the History of Mathematics?". Isis. 102 (3): 475–480. doi:10.1086/661620. ISSN 0021-1753. MR 2884913. PMID 22073771. S2CID 21629993.
- ^ a b c d e f Kleiner, Israel (December 1991). "Rigor and Proof in Mathematics: A Historical Perspective". Mathematics Magazine. 64 (5). Taylor & Francis, Ltd.: 291–314. doi:10.1080/0025570X.1991.11977625. eISSN 1930-0980. ISSN 0025-570X. JSTOR 2690647. LCCN 47003192. MR 1141557. OCLC 1756877. S2CID 7787171.
- ^ Bell, E. T. (1945) [1940]. "General Prospectus". The Development of Mathematics (2nd ed.). Dover Publications. p. 3. ISBN 978-0-486-27239-9. LCCN 45010599. OCLC 523284.
... mathematics has come down to the present by the two main streams of number and form. The first carried along arithmetic and algebra, the second, geometry.
{{cite book}}: ISBN / Date incompatibility (help) - ^ Tiwari, Sarju (1992). "A Mirror of Civilization". Mathematics in History, Culture, Philosophy, and Science (1st ed.). New Delhi, India: Mittal Publications. p. 27. ISBN 978-81-7099-404-6. LCCN 92909575. OCLC 28115124.
It is unfortunate that two curses of mathematics--Numerology and Astrology were also born with it and have been more acceptable to the masses than mathematics itself.
- ^ Restivo, Sal (1992). "Mathematics from the Ground Up". In Bunge, Mario (ed.). Mathematics in Society and History. Episteme. Vol. 20. Kluwer Academic Publishers. p. 14. ISBN 0-7923-1765-3. LCCN 25709270. OCLC 92013695.
- ^ Musielak, Dora (2022). Leonhard Euler and the Foundations of Celestial Mechanics. History of Physics. Springer International Publishing. doi:10.1007/978-3-031-12322-1. eISSN 2730-7557. ISBN 978-3-031-12321-4. ISSN 2730-7549. OCLC 1332780664. S2CID 253240718.
- ^ Biggs, N. L. (May 1979). "The roots of combinatorics". Historia Mathematica. 6 (2): 109–136. doi:10.1016/0315-0860(79)90074-0. eISSN 1090-249X. ISSN 0315-0860. LCCN 75642280. OCLC 2240703.
- ^ a b Warner, Evan. "Splash Talk: The Foundational Crisis of Mathematics" (PDF). Columbia University. Archived from the original (PDF) on March 22, 2023. Retrieved February 3, 2024.
- ^ Dunne, Edward; Hulek, Klaus (March 2020). "Mathematics Subject Classification 2020" (PDF). Notices of the American Mathematical Society. 67 (3): 410–411. doi:10.1090/noti2052. eISSN 1088-9477. ISSN 0002-9920. LCCN sf77000404. OCLC 1480366. Archived (PDF) from the original on August 3, 2021. Retrieved February 3, 2024.
The new MSC contains 63 two-digit classifications, 529 three-digit classifications, and 6,006 five-digit classifications.
- ^ a b c d e f g h "MSC2020-Mathematics Subject Classification System" (PDF). zbMath. Associate Editors of Mathematical Reviews and zbMATH. Archived (PDF) from the original on January 2, 2024. Retrieved February 3, 2024.
- ^ LeVeque, William J. (1977). "Introduction". Fundamentals of Number Theory. Addison-Wesley Publishing Company. pp. 1–30. ISBN 0-201-04287-8. LCCN 76055645. OCLC 3519779. S2CID 118560854.
- ^ Goldman, Jay R. (1998). "The Founding Fathers". The Queen of Mathematics: A Historically Motivated Guide to Number Theory. Wellesley, MA: A K Peters. pp. 2–3. doi:10.1201/9781439864623. ISBN 1-56881-006-7. LCCN 94020017. OCLC 30437959. S2CID 118934517.
- ^ Weil, André (1983). Number Theory: An Approach Through History From Hammurapi to Legendre. Birkhäuser Boston. pp. 2–3. doi:10.1007/978-0-8176-4571-7. ISBN 0-8176-3141-0. LCCN 83011857. OCLC 9576587. S2CID 117789303.
- ^ Kleiner, Israel (March 2000). "From Fermat to Wiles: Fermat's Last Theorem Becomes a Theorem". Elemente der Mathematik. 55 (1): 19–37. doi:10.1007/PL00000079. eISSN 1420-8962. ISSN 0013-6018. LCCN 66083524. OCLC 1567783. S2CID 53319514.
- ^ Wang, Yuan (2002). The Goldbach Conjecture. Series in Pure Mathematics. Vol. 4 (2nd ed.). World Scientific. pp. 1–18. doi:10.1142/5096. ISBN 981-238-159-7. LCCN 2003268597. OCLC 51533750. S2CID 14555830.
- ^ a b c Straume, Eldar (September 4, 2014). "A Survey of the Development of Geometry up to 1870". arXiv:1409.1140 [math.HO].
- ^ Hilbert, David (1902). The Foundations of Geometry. Open Court Publishing Company. p. 1. doi:10.1126/science.16.399.307. LCCN 02019303. OCLC 996838. S2CID 238499430. Retrieved February 6, 2024.

- ^ Hartshorne, Robin (2000). "Euclid's Geometry". Geometry: Euclid and Beyond. Springer New York. pp. 9–13. ISBN 0-387-98650-2. LCCN 99044789. OCLC 42290188. Retrieved February 7, 2024.
- ^ Boyer, Carl B. (2004) [1956]. "Fermat and Descartes". History of Analytic Geometry. Dover Publications. pp. 74–102. ISBN 0-486-43832-5. LCCN 2004056235. OCLC 56317813.
- ^ Stump, David J. (1997). "Reconstructing the Unity of Mathematics circa 1900" (PDF). Perspectives on Science. 5 (3): 383–417. doi:10.1162/posc_a_00532. eISSN 1530-9274. ISSN 1063-6145. LCCN 94657506. OCLC 26085129. S2CID 117709681. Archived (PDF) from the original on February 8, 2024. Retrieved February 8, 2024.
- ^ O'Connor, J. J.; Robertson, E. F. (February 1996). "Non-Euclidean geometry". MacTuror. Scotland, UK: University of St. Andrews. Archived from the original on November 6, 2022. Retrieved February 8, 2024.
- ^ Joyner, David (2008). "The (legal) Rubik's Cube group". Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys (2nd ed.). Johns Hopkins University Press. pp. 219–232. ISBN 978-0-8018-9012-3. LCCN 2008011322. OCLC 213765703.
- ^ Christianidis, Jean; Oaks, Jeffrey (May 2013). "Practicing algebra in late antiquity: The problem-solving of Diophantus of Alexandria". Historia Mathematica. 40 (2): 127–163. doi:10.1016/j.hm.2012.09.001. eISSN 1090-249X. ISSN 0315-0860. LCCN 75642280. OCLC 2240703. S2CID 121346342.
- ^ Kleiner 2007, "History of Classical Algebra" pp. 3–5.
- ^ Shane, David (2022). "Figurate Numbers: A Historical Survey of an Ancient Mathematics" (PDF). Methodist University. p. 20. Archived (PDF) from the original on June 5, 2024. Retrieved June 13, 2024.
In his work, Diophantus focused on deducing the arithmetic properties of figurate numbers, such as deducing the number of sides, the different ways a number can be expressed as a figurate number, and the formulation of the arithmetic progressions.
- ^ Overbay, Shawn; Schorer, Jimmy; Conger, Heather. "Al-Khwarizmi". University of Kentucky. Archived from the original on June 29, 2024. Retrieved June 13, 2024.
- ^ Lim, Lisa (December 21, 2018). "Where the x we use in algebra came from, and the X in Xmas". South China Morning Post. Archived from the original on December 22, 2018. Retrieved February 8, 2024.
- ^ Berntjes, Sonja. "Algebra". Encyclopaedia of Islam Online (3rd ed.). ISSN 1573-3912. LCCN 2007238847. OCLC 56713464. Archived from the original on January 12, 2025. Retrieved June 13, 2024.
- ^ Oaks, Jeffery A. (2018). "François Viète's revolution in algebra" (PDF). Archive for History of Exact Sciences. 72 (3): 245–302. doi:10.1007/s00407-018-0208-0. eISSN 1432-0657. ISSN 0003-9519. LCCN 63024699. OCLC 1482042. S2CID 125704699. Archived (PDF) from the original on November 8, 2022. Retrieved February 8, 2024.
- ^ "Variable in Maths". GeeksforGeeks. April 24, 2024. Archived from the original on June 1, 2024. Retrieved June 13, 2024.
- ^ Kleiner 2007, "History of Linear Algebra" pp. 79–101.
- ^ Corry, Leo (2004). "Emmy Noether: Ideals and Structures". Modern Algebra and the Rise of Mathematical Structures (2nd revised ed.). Germany: Birkhäuser Basel. pp. 247–252. ISBN 3-7643-7002-5. LCCN 2004556211. OCLC 51234417. Retrieved February 8, 2024.
- ^ Riche, Jacques (2007). "From Universal Algebra to Universal Logic". In Beziau, J. Y.; Costa-Leite, Alexandre (eds.). Perspectives on Universal Logic. Milano, Italy: Polimetrica International Scientific Publisher. pp. 3–39. ISBN 978-88-7699-077-9. OCLC 647049731. Retrieved February 8, 2024.
- ^ Krömer, Ralph (2007). Tool and Object: A History and Philosophy of Category Theory. Science Networks – Historical Studies. Vol. 32. Germany: Springer Science & Business Media. pp. xxi–xxv, 1–91. ISBN 978-3-7643-7523-2. LCCN 2007920230. OCLC 85242858. Retrieved February 8, 2024.
- ^ Guicciardini, Niccolo (2017). "The Newton–Leibniz Calculus Controversy, 1708–1730" (PDF). In Schliesser, Eric; Smeenk, Chris (eds.). The Oxford Handbook of Newton. Oxford Handbooks. Oxford University Press. doi:10.1093/oxfordhb/9780199930418.013.9. ISBN 978-0-19-993041-8. OCLC 975829354. Archived (PDF) from the original on November 9, 2022. Retrieved February 9, 2024.
- ^ O'Connor, J. J.; Robertson, E. F. (September 1998). "Leonhard Euler". MacTutor. Scotland, UK: University of St Andrews. Archived from the original on November 9, 2022. Retrieved February 9, 2024.
- ^ "Calculus (Differential and Integral Calculus with Examples)". Byju's. Retrieved June 13, 2024.
- ^ Franklin, James (July 2017). "Discrete and Continuous: A Fundamental Dichotomy in Mathematics". Journal of Humanistic Mathematics. 7 (2): 355–378. doi:10.5642/jhummath.201702.18. hdl:1959.4/unsworks_53212. ISSN 2159-8118. LCCN 2011202231. OCLC 700943261. S2CID 6945363. Archived from the original on March 10, 2024. Retrieved February 9, 2024.
- ^ Maurer, Stephen B. (1997). "What is Discrete Mathematics? The Many Answers". In Rosenstein, Joseph G.; Franzblau, Deborah S.; Roberts, Fred S. (eds.). Discrete Mathematics in the Schools. DIMACS: Series in Discrete Mathematics and Theoretical Computer Science. Vol. 36. American Mathematical Society. pp. 121–124. doi:10.1090/dimacs/036/13. ISBN 0-8218-0448-0. ISSN 1052-1798. LCCN 97023277. OCLC 37141146. S2CID 67358543. Retrieved February 9, 2024.
- ^ Hales, Thomas C. (2014). "Turing's Legacy: Developments from Turing's Ideas in Logic". In Downey, Rod (ed.). Turing's Legacy. Lecture Notes in Logic. Vol. 42. Cambridge University Press. pp. 260–261. doi:10.1017/CBO9781107338579.001. ISBN 978-1-107-04348-0. LCCN 2014000240. OCLC 867717052. S2CID 19315498. Retrieved February 9, 2024.
- ^ Sipser, Michael (July 1992). The History and Status of the P versus NP Question. STOC '92: Proceedings of the twenty-fourth annual ACM symposium on Theory of Computing. pp. 603–618. doi:10.1145/129712.129771. S2CID 11678884.
- ^ Ewald, William (November 17, 2018). "The Emergence of First-Order Logic". Stanford Encyclopedia of Philosophy. ISSN 1095-5054. LCCN sn97004494. OCLC 37550526. Retrieved June 14, 2024.
- ^ Ferreirós, José (June 18, 2020) [First published April 10, 2007]. "The Early Development of Set Theory". Stanford Encyclopedia of Philosophy. ISSN 1095-5054. LCCN sn97004494. OCLC 37550526. Archived from the original on May 12, 2021. Retrieved June 14, 2024.
- ^ Ferreirós, José (December 2001). "The Road to Modern Logic—An Interpretation" (PDF). The Bulletin of Symbolic Logic. 7 (4): 441–484. doi:10.2307/2687794. eISSN 1943-5894. hdl:11441/38373. ISSN 1079-8986. JSTOR 2687794. LCCN 95652899. OCLC 31616719. S2CID 43258676. Archived from the original (PDF) on February 2, 2023. Retrieved June 14, 2024.
- ^ Wolchover, Natalie, ed. (November 26, 2013). "Dispute over Infinity Divides Mathematicians". Quanta Magazine. Retrieved June 14, 2024.
- ^ Zhuang, Chaohui. "Wittgenstein's analysis on Cantor's diagonal argument" (DOC). PhilArchive. Retrieved June 14, 2024.
- ^ Tanswell, Fenner Stanley (2024). Mathematical Rigour and Informal Proof. Cambridge Elements in the Philosophy of Mathematics. Cambridge University Press. doi:10.1017/9781009325110. eISSN 2399-2883. ISBN 978-1-00-949438-0. ISSN 2514-3808. OCLC 1418750041.
- ^ Avigad, Jeremy; Reck, Erich H. (December 11, 2001). ""Clarifying the nature of the infinite": the development of metamathematics and proof theory" (PDF). Carnegie Mellon University. Archived (PDF) from the original on October 9, 2022. Retrieved June 14, 2024.
- ^ Hamilton, Alan G. (1982). Numbers, Sets and Axioms: The Apparatus of Mathematics. Cambridge University Press. pp. 3–4. ISBN 978-0-521-28761-6. Retrieved November 12, 2022.
- ^ Snapper, Ernst (September 1979). "The Three Crises in Mathematics: Logicism, Intuitionism, and Formalism". Mathematics Magazine. 52 (4): 207–216. doi:10.2307/2689412. ISSN 0025-570X. JSTOR 2689412.
- ^ a b Raatikainen, Panu (October 2005). "On the Philosophical Relevance of Gödel's Incompleteness Theorems". Revue Internationale de Philosophie. 59 (4): 513–534. doi:10.3917/rip.234.0513. JSTOR 23955909. S2CID 52083793. Archived from the original on November 12, 2022. Retrieved November 12, 2022.
- ^ Moschovakis, Joan (September 4, 2018). "Intuitionistic Logic". Stanford Encyclopedia of Philosophy. Archived from the original on December 16, 2022. Retrieved November 12, 2022.
- ^ McCarty, Charles (2006). "At the Heart of Analysis: Intuitionism and Philosophy". Philosophia Scientiæ, Cahier spécial 6: 81–94. doi:10.4000/philosophiascientiae.411.
- ^ Halpern, Joseph; Harper, Robert; Immerman, Neil; Kolaitis, Phokion; Vardi, Moshe; Vianu, Victor (2001). "On the Unusual Effectiveness of Logic in Computer Science" (PDF). Archived (PDF) from the original on March 3, 2021. Retrieved January 15, 2021.
- ^ Rouaud, Mathieu (April 2017) [First published July 2013]. Probability, Statistics and Estimation (PDF). p. 10. Archived (PDF) from the original on October 9, 2022. Retrieved February 13, 2024.
- ^ Rao, C. Radhakrishna (1997) [1989]. Statistics and Truth: Putting Chance to Work (2nd ed.). World Scientific. pp. 3–17, 63–70. ISBN 981-02-3111-3. LCCN 97010349. MR 1474730. OCLC 36597731.
- ^ Rao, C. Radhakrishna (1981). "Foreword". In Arthanari, T.S.; Dodge, Yadolah (eds.). Mathematical programming in statistics. Wiley Series in Probability and Mathematical Statistics. New York: Wiley. pp. vii–viii. ISBN 978-0-471-08073-2. LCCN 80021637. MR 0607328. OCLC 6707805.
- ^ Whittle 1994, pp. 10–11, 14–18.
- ^ Marchuk, Gurii Ivanovich (April 2020). "G I Marchuk's plenary: ICM 1970". MacTutor. School of Mathematics and Statistics, University of St Andrews, Scotland. Archived from the original on November 13, 2022. Retrieved November 13, 2022.
- ^ Johnson, Gary M.; Cavallini, John S. (September 1991). Phua, Kang Hoh; Loe, Kia Fock (eds.). Grand Challenges, High Performance Computing, and Computational Science. Singapore Supercomputing Conference'90: Supercomputing For Strategic Advantage. World Scientific. p. 28. LCCN 91018998. Retrieved November 13, 2022.
- ^ Trefethen, Lloyd N. (2008). "Numerical Analysis". In Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.). The Princeton Companion to Mathematics (PDF). Princeton University Press. pp. 604–615. ISBN 978-0-691-11880-2. LCCN 2008020450. MR 2467561. OCLC 227205932. Archived (PDF) from the original on March 7, 2023. Retrieved February 15, 2024.
- ^
- Cresswell 2021, § Mathematics
- Perisho 1965, p. 64
- ^ Perisho, Margaret W. (Spring 1965). "The Etymology of Mathematical Terms". Pi Mu Epsilon Journal. 4 (2): 62–66. ISSN 0031-952X. JSTOR 24338341. LCCN 58015848. OCLC 1762376.
- ^ Boas, Ralph P. (1995). "What Augustine Didn't Say About Mathematicians". In Alexanderson, Gerald L.; Mugler, Dale H. (eds.). Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories. Mathematical Association of America. p. 257. ISBN 978-0-88385-323-8. LCCN 94078313. OCLC 633018890.
- ^ The Oxford Dictionary of English Etymology, Oxford English Dictionary, sub "mathematics", "mathematic", "mathematics".
- ^ "Maths (Noun)". Oxford English Dictionary. Oxford University Press. Archived from the original on January 25, 2024. Retrieved January 25, 2024.
- ^ "Math (Noun³)". Oxford English Dictionary. Oxford University Press. Archived from the original on April 4, 2020. Retrieved January 25, 2024.
- ^ See, for example, Wilder, Raymond L. Evolution of Mathematical Concepts; an Elementary Study. passim.
- ^ Zaslavsky, Claudia (1999). Africa Counts: Number and Pattern in African Culture. Chicago Review Press. ISBN 978-1-61374-115-3. OCLC 843204342.
- ^ Kline 1990, Chapter 1.
- ^ Mesopotamia[dead link] pg 10. Retrieved June 1, 2024
- ^ Boyer 1991, "Mesopotamia" pp. 24–27.
- ^ Heath, Thomas Little (1981) [1921]. A History of Greek Mathematics: From Thales to Euclid. New York: Dover Publications. p. 1. ISBN 978-0-486-24073-2.
- ^ Mueller, I. (1969). "Euclid's Elements and the Axiomatic Method". The British Journal for the Philosophy of Science. 20 (4): 289–309. doi:10.1093/bjps/20.4.289. ISSN 0007-0882. JSTOR 686258.
- ^ Boyer 1991, "Euclid of Alexandria" p. 119.
- ^ Boyer 1991, "Archimedes of Syracuse" p. 120.
- ^ Boyer 1991, "Archimedes of Syracuse" p. 130.
- ^ Boyer 1991, "Apollonius of Perga" p. 145.
- ^ Boyer 1991, "Greek Trigonometry and Mensuration" p. 162.
- ^ Boyer 1991, "Revival and Decline of Greek Mathematics" p. 180.
- ^ Ore, Øystein (1988). Number Theory and Its History. Courier Corporation. pp. 19–24. ISBN 978-0-486-65620-5. Retrieved November 14, 2022.
- ^ Singh, A. N. (January 1936). "On the Use of Series in Hindu Mathematics". Osiris. 1: 606–628. doi:10.1086/368443. JSTOR 301627. S2CID 144760421.
- ^ Kolachana, A.; Mahesh, K.; Ramasubramanian, K. (2019). "Use of series in India". Studies in Indian Mathematics and Astronomy. Sources and Studies in the History of Mathematics and Physical Sciences. Singapore: Springer. pp. 438–461. doi:10.1007/978-981-13-7326-8_20. ISBN 978-981-13-7325-1. S2CID 190176726.
- ^ Saliba, George (1994). A history of Arabic astronomy: planetary theories during the golden age of Islam. New York University Press. ISBN 978-0-8147-7962-0. OCLC 28723059.
- ^ Faruqi, Yasmeen M. (2006). "Contributions of Islamic scholars to the scientific enterprise". International Education Journal. 7 (4). Shannon Research Press: 391–399. Archived from the original on November 14, 2022. Retrieved November 14, 2022.
- ^ Lorch, Richard (June 2001). "Greek-Arabic-Latin: The Transmission of Mathematical Texts in the Middle Ages" (PDF). Science in Context. 14 (1–2). Cambridge University Press: 313–331. doi:10.1017/S0269889701000114. S2CID 146539132. Archived (PDF) from the original on December 17, 2022. Retrieved December 5, 2022.
- ^ Kent, Benjamin (2022). History of Science (PDF). Vol. 2. Bibliotex Digital Library. ISBN 978-1-984668-67-7. Archived (PDF) from the original on June 16, 2024. Retrieved June 16, 2024.
- ^ Archibald, Raymond Clare (January 1949). "History of Mathematics After the Sixteenth Century". The American Mathematical Monthly. Part 2: Outline of the History of Mathematics. 56 (1): 35–56. doi:10.2307/2304570. JSTOR 2304570.
- ^ Sevryuk 2006, pp. 101–109.
- ^ Wolfram, Stephan (October 2000). Mathematical Notation: Past and Future. MathML and Math on the Web: MathML International Conference 2000, Urbana Champaign, USA. Archived from the original on November 16, 2022. Retrieved February 3, 2024.
- ^ Douglas, Heather; Headley, Marcia Gail; Hadden, Stephanie; LeFevre, Jo-Anne (December 3, 2020). "Knowledge of Mathematical Symbols Goes Beyond Numbers". Journal of Numerical Cognition. 6 (3): 322–354. doi:10.5964/jnc.v6i3.293. eISSN 2363-8761. S2CID 228085700.
- ^ Letourneau, Mary; Wright Sharp, Jennifer (October 2017). "AMS Style Guide" (PDF). American Mathematical Society. p. 75. Archived (PDF) from the original on December 8, 2022. Retrieved February 3, 2024.
- ^ Jansen, Anthony R.; Marriott, Kim; Yelland, Greg W. (2000). "Constituent Structure in Mathematical Expressions" (PDF). Proceedings of the Annual Meeting of the Cognitive Science Society. 22. University of California Merced. eISSN 1069-7977. OCLC 68713073. Archived (PDF) from the original on November 16, 2022. Retrieved February 3, 2024.
- ^ Rossi, Richard J. (2006). Theorems, Corollaries, Lemmas, and Methods of Proof. Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts. John Wiley & Sons. pp. 1–14, 47–48. ISBN 978-0-470-04295-3. LCCN 2006041609. OCLC 64085024.
- ^ "Earliest Uses of Some Words of Mathematics". MacTutor. Scotland, UK: University of St. Andrews. Archived from the original on September 29, 2022. Retrieved February 3, 2024.
- ^ Silver, Daniel S. (November–December 2017). "The New Language of Mathematics". The American Scientist. 105 (6). Sigma Xi: 364–371. doi:10.1511/2017.105.6.364. ISSN 0003-0996. LCCN 43020253. OCLC 1480717. S2CID 125455764.
- ^ Bellomo, Nicola; Preziosi, Luigi (December 22, 1994). Modelling Mathematical Methods and Scientific Computation. Mathematical Modeling. Vol. 1. CRC Press. p. 1. ISBN 978-0-8493-8331-1. Retrieved November 16, 2022.
- ^ Hennig, Christian (2010). "Mathematical Models and Reality: A Constructivist Perspective". Foundations of Science. 15: 29–48. doi:10.1007/s10699-009-9167-x. S2CID 6229200. Retrieved November 17, 2022.
- ^ Frigg, Roman; Hartmann, Stephan (February 4, 2020). "Models in Science". Stanford Encyclopedia of Philosophy. Archived from the original on November 17, 2022. Retrieved November 17, 2022.
- ^ Stewart, Ian (2018). "Mathematics, Maps, and Models". In Wuppuluri, Shyam; Doria, Francisco Antonio (eds.). The Map and the Territory: Exploring the Foundations of Science, Thought and Reality. The Frontiers Collection. Springer. pp. 345–356. doi:10.1007/978-3-319-72478-2_18. ISBN 978-3-319-72478-2. Retrieved November 17, 2022.
- ^ "The science checklist applied: Mathematics". Understanding Science. University of California, Berkeley. Archived from the original on October 27, 2019. Retrieved October 27, 2019.
- ^ Mackay, A. L. (1991). Dictionary of Scientific Quotations. London: Taylor & Francis. p. 100. ISBN 978-0-7503-0106-0. Retrieved March 19, 2023.
- ^ Bishop, Alan (1991). "Environmental activities and mathematical culture". Mathematical Enculturation: A Cultural Perspective on Mathematics Education. Norwell, Massachusetts: Kluwer Academic Publishers. pp. 20–59. ISBN 978-0-7923-1270-3. Retrieved April 5, 2020.
- ^ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. p. 228. ISBN 978-0-387-98269-4.
- ^ Nickles, Thomas (2013). "The Problem of Demarcation". Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. Chicago: The University of Chicago Press. p. 104. ISBN 978-0-226-05182-6.
- ^ Pigliucci, Massimo (2014). "Are There 'Other' Ways of Knowing?". Philosophy Now. Archived from the original on May 13, 2020. Retrieved April 6, 2020.
- ^ a b Ferreirós, J. (2007). "Ό Θεὸς Άριθμητίζει: The Rise of Pure Mathematics as Arithmetic with Gauss". In Goldstein, Catherine; Schappacher, Norbert; Schwermer, Joachim (eds.). The Shaping of Arithmetic after C.F. Gauss's Disquisitiones Arithmeticae. Springer Science & Business Media. pp. 235–268. ISBN 978-3-540-34720-0.
- ^ Kuhn, Thomas S. (1976). "Mathematical vs. Experimental Traditions in the Development of Physical Science". The Journal of Interdisciplinary History. 7 (1). The MIT Press: 1–31. doi:10.2307/202372. JSTOR 202372.
- ^ Asper, Markus (2009). "The two cultures of mathematics in ancient Greece". In Robson, Eleanor; Stedall, Jacqueline (eds.). The Oxford Handbook of the History of Mathematics. Oxford Handbooks in Mathematics. OUP Oxford. pp. 107–132. ISBN 978-0-19-921312-2. Retrieved November 18, 2022.
- ^ Gozwami, Pinkimani; Singh, Madan Mohan (2019). "Integer Factorization Problem". In Ahmad, Khaleel; Doja, M. N.; Udzir, Nur Izura; Singh, Manu Pratap (eds.). Emerging Security Algorithms and Techniques. CRC Press. pp. 59–60. ISBN 978-0-8153-6145-9. LCCN 2019010556. OCLC 1082226900.
- ^ Maddy, P. (2008). "How applied mathematics became pure" (PDF). The Review of Symbolic Logic. 1 (1): 16–41. doi:10.1017/S1755020308080027. S2CID 18122406. Archived (PDF) from the original on August 12, 2017. Retrieved November 19, 2022.
- ^ Silver, Daniel S. (2017). "In Defense of Pure Mathematics". In Pitici, Mircea (ed.). The Best Writing on Mathematics, 2016. Princeton University Press. pp. 17–26. ISBN 978-0-691-17529-4. Retrieved November 19, 2022.
- ^ Parshall, Karen Hunger (2022). "The American Mathematical Society and Applied Mathematics from the 1920s to the 1950s: A Revisionist Account". Bulletin of the American Mathematical Society. 59 (3): 405–427. doi:10.1090/bull/1754. S2CID 249561106. Archived from the original on November 20, 2022. Retrieved November 20, 2022.
- ^ Stolz, Michael (2002). "The History Of Applied Mathematics And The History Of Society". Synthese. 133 (1–2): 43–57. doi:10.1023/A:1020823608217. S2CID 34271623. Retrieved November 20, 2022.
- ^ Lin, C. C . (March 1976). "On the role of applied mathematics". Advances in Mathematics. 19 (3): 267–288. doi:10.1016/0001-8708(76)90024-4.
- ^ Peressini, Anthony (September 1999). Applying Pure Mathematics (PDF). Philosophy of Science. Proceedings of the 1998 Biennial Meetings of the Philosophy of Science Association. Part I: Contributed Papers. Vol. 66. pp. S1 – S13. JSTOR 188757. Archived (PDF) from the original on January 2, 2024. Retrieved November 30, 2022.
- ^ Lützen, J. (2011). "Examples and reflections on the interplay between mathematics and physics in the 19th and 20th century". In Schlote, K. H.; Schneider, M. (eds.). Mathematics meets physics: A contribution to their interaction in the 19th and the first half of the 20th century. Frankfurt am Main: Verlag Harri Deutsch. Archived from the original on March 23, 2023. Retrieved November 19, 2022.
- ^ Marker, Dave (July 1996). "Model theory and exponentiation". Notices of the American Mathematical Society. 43 (7): 753–759. Archived from the original on March 13, 2014. Retrieved November 19, 2022.
- ^ Chen, Changbo; Maza, Marc Moreno (August 2014). Cylindrical Algebraic Decomposition in the RegularChains Library. International Congress on Mathematical Software 2014. Lecture Notes in Computer Science. Vol. 8592. Berlin: Springer. doi:10.1007/978-3-662-44199-2_65. Retrieved November 19, 2022.
- ^ Pérez-Escobar, José Antonio; Sarikaya, Deniz (2021). "Purifying applied mathematics and applying pure mathematics: how a late Wittgensteinian perspective sheds light onto the dichotomy". European Journal for Philosophy of Science. 12 (1): 1–22. doi:10.1007/s13194-021-00435-9. S2CID 245465895.
- ^ Takase, M. (2014). "Pure Mathematics and Applied Mathematics are Inseparably Intertwined: Observation of the Early Analysis of the Infinity". A Mathematical Approach to Research Problems of Science and Technology. Mathematics for Industry. Vol. 5. Tokyo: Springer. pp. 393–399. doi:10.1007/978-4-431-55060-0_29. ISBN 978-4-431-55059-4. Retrieved November 20, 2022.
- ^ Sarukkai, Sundar (February 10, 2005). "Revisiting the 'unreasonable effectiveness' of mathematics". Current Science. 88 (3): 415–423. JSTOR 24110208.
- ^ Wagstaff, Samuel S. Jr. (2021). "History of Integer Factoring" (PDF). In Bos, Joppe W.; Stam, Martijn (eds.). Computational Cryptography, Algorithmic Aspects of Cryptography, A Tribute to AKL. London Mathematical Society Lecture Notes Series 469. Cambridge University Press. pp. 41–77. Archived (PDF) from the original on November 20, 2022. Retrieved November 20, 2022.
- ^ "Curves: Ellipse". MacTutor. School of Mathematics and Statistics, University of St Andrews, Scotland. Archived from the original on October 14, 2022. Retrieved November 20, 2022.
- ^ Mukunth, Vasudevan (September 10, 2015). "Beyond the Surface of Einstein's Relativity Lay a Chimerical Geometry". The Wire. Archived from the original on November 20, 2022. Retrieved November 20, 2022.
- ^ Wilson, Edwin B.; Lewis, Gilbert N. (November 1912). "The Space-Time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics". Proceedings of the American Academy of Arts and Sciences. 48 (11): 389–507. doi:10.2307/20022840. JSTOR 20022840.
- ^ a b c Borel, Armand (1983). "Mathematics: Art and Science". The Mathematical Intelligencer. 5 (4). Springer: 9–17. doi:10.4171/news/103/8. ISSN 1027-488X.
- ^ Hanson, Norwood Russell (November 1961). "Discovering the Positron (I)". The British Journal for the Philosophy of Science. 12 (47). The University of Chicago Press: 194–214. doi:10.1093/bjps/xiii.49.54. JSTOR 685207.
- ^ Ginammi, Michele (February 2016). "Avoiding reification: Heuristic effectiveness of mathematics and the prediction of the Ω– particle". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 53: 20–27. Bibcode:2016SHPMP..53...20G. doi:10.1016/j.shpsb.2015.12.001.
- ^ Wagh, Sanjay Moreshwar; Deshpande, Dilip Abasaheb (September 27, 2012). Essentials of Physics. PHI Learning Pvt. Ltd. p. 3. ISBN 978-81-203-4642-0. Retrieved January 3, 2023.
- ^ Atiyah, Michael (1990). On the Work of Edward Witten (PDF). Proceedings of the International Congress of Mathematicians. p. 31. Archived from the original (PDF) on September 28, 2013. Retrieved December 29, 2022.
- ^ "Course 18C Mathematics with Computer Science". math.mit.edu. Retrieved June 1, 2024.
- ^ "Theoretical Computer Science". math.mit.edu. Retrieved June 1, 2024.
- ^ "Real-Life Applications of Discrete Mathematics". GeeksforGeeks. April 8, 2024. Archived from the original on May 19, 2024. Retrieved May 19, 2024.
- ^ Hales, Thomas; Adams, Mark; Bauer, Gertrud; Dang, Tat Dat; Harrison, John; Hoang, Le Truong; Kaliszyk, Cezary; Magron, Victor; Mclaughlin, Sean; Nguyen, Tat Thang; Nguyen, Quang Truong; Nipkow, Tobias; Obua, Steven; Pleso, Joseph; Rute, Jason; Solovyev, Alexey; Ta, Thi Hoai An; Tran, Nam Trung; Trieu, Thi Diep; Urban, Josef; Vu, Ky; Zumkeller, Roland (2017). "A Formal Proof of the Kepler Conjecture". Forum of Mathematics, Pi. 5 e2. doi:10.1017/fmp.2017.1. hdl:2066/176365. ISSN 2050-5086. S2CID 216912822. Archived from the original on December 4, 2020. Retrieved February 25, 2023.
- ^ a b c Millstein, Roberta (September 8, 2016). "Probability in Biology: The Case of Fitness" (PDF). In Hájek, Alan; Hitchcock, Christopher (eds.). The Oxford Handbook of Probability and Philosophy. pp. 601–622. doi:10.1093/oxfordhb/9780199607617.013.27. Archived (PDF) from the original on March 7, 2023. Retrieved December 29, 2022.
- ^ See for example Anne Laurent, Roland Gamet, Jérôme Pantel, Tendances nouvelles en modélisation pour l'environnement, actes du congrès «Programme environnement, vie et sociétés» 15–17 janvier 1996, CNRS
- ^ Bouleau 1999, pp. 282–283.
- ^ Bouleau 1999, p. 285.
- ^ "1.4: The Lotka-Volterra Predator-Prey Model". Mathematics LibreTexts. January 5, 2022. Archived from the original on December 29, 2022. Retrieved December 29, 2022.
- ^ Salsburg, David (August 17, 1992). "Commentary" (PDF). The Use of Statistical Methods in the Analysis of Clinical Studies. 46: 17. Archived (PDF) from the original on June 1, 2024. Retrieved June 1, 2024.
- ^ National Research Council (2003). "8". Beyond the Molecular Frontier: Challenges for Chemistry and Chemical Engineering. NAP.edu. pp. 71–73. doi:10.17226/10633. ISBN 978-0-309-16839-7. PMID 25032300.
- ^ "Catastrophe Models (Property)". content.naic.org. Archived from the original on May 19, 2024. Retrieved May 19, 2024.
- ^ "MAM2001 Essay". ww2.amstat.org. Archived from the original on May 19, 2024. Retrieved May 19, 2024.
- ^ Hill, Mullica (September 7, 2022). "HOW MATH IS USED IN WEATHER FORECASTING". mathnasium.com. Archived from the original on May 19, 2024. Retrieved May 19, 2024.
- ^ "Using Mathematical Models to Investigate Planetary Habitability" (PDF). NASA. Archived (PDF) from the original on May 19, 2024. Retrieved May 19, 2024.
- ^ Edling, Christofer R. (2002). "Mathematics in Sociology". Annual Review of Sociology. 28 (1): 197–220. doi:10.1146/annurev.soc.28.110601.140942. ISSN 0360-0572. Archived from the original on November 15, 2021. Retrieved September 30, 2023.
- ^ Batchelder, William H. (January 1, 2015). "Mathematical Psychology: History". In Wright, James D. (ed.). International Encyclopedia of the Social & Behavioral Sciences (Second Edition). Oxford: Elsevier. pp. 808–815. ISBN 978-0-08-097087-5. Archived from the original on February 17, 2023. Retrieved September 30, 2023.
- ^ a b Zak, Paul J. (2010). Moral Markets: The Critical Role of Values in the Economy. Princeton University Press. p. 158. ISBN 978-1-4008-3736-6. Retrieved January 3, 2023.
- ^ Levin, Jonathan; Milgrom, Paul (September 2004). Introduction to Choice Theory (PDF).
- ^ Kremer, Michael; Rao, Gautam; Schilbach, Frank (2019). "Chapter 5 Behavioral development economics". Handbook of Behavioral Economics: Applications and Foundations (PDF). Vol. 2. Archived (PDF) from the original on June 2, 2024. Retrieved June 2, 2024.
- ^ "Mathematics". mdpi.com.
- ^ "Kondratiev, Nikolai Dmitrievich | Encyclopedia.com". www.encyclopedia.com. Archived from the original on July 1, 2016. Retrieved December 29, 2022.
- ^ "Mathématique de l'histoire-géometrie et cinématique. Lois de Brück. Chronologie géodésique de la Bible., by Charles LAGRANGE et al. | The Online Books Page". onlinebooks.library.upenn.edu. Archived from the original on January 3, 2024. Retrieved January 3, 2024.
- ^ "Cliodynamics: a science for predicting the future". ZDNet. Archived from the original on December 29, 2022. Retrieved December 29, 2022.
- ^ Sokal, Alan; Jean Bricmont (1998). Fashionable Nonsense. New York: Picador. ISBN 978-0-312-19545-8. OCLC 39605994.
- ^ "Biden's Misleading Unemployment Statistic – FactCheck.org". January 27, 2023. Archived from the original on June 2, 2024. Retrieved June 2, 2024.
- ^ "Modern Macroeconomic Models as Tools for Economic Policy | Federal Reserve Bank of Minneapolis". minneapolisfed.org. Archived from the original on August 3, 2024. Retrieved June 2, 2024.
- ^ Balaguer, Mark (2016). "Platonism in Metaphysics". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Spring 2016 ed.). Metaphysics Research Lab, Stanford University. Archived from the original on January 30, 2022. Retrieved April 2, 2022.
- ^ See White, L. (1947). "The locus of mathematical reality: An anthropological footnote". Philosophy of Science. 14 (4): 289–303. doi:10.1086/286957. S2CID 119887253. 189303; also in Newman, J. R. (1956). The World of Mathematics. Vol. 4. New York: Simon and Schuster. pp. 2348–2364.
- ^ Dorato, Mauro (2005). "Why are laws mathematical?" (PDF). The Software of the Universe, An Introduction to the History and Philosophy of Laws of Nature. Ashgate. pp. 31–66. ISBN 978-0-7546-3994-7. Archived (PDF) from the original on August 17, 2023. Retrieved December 5, 2022.
- ^ Mura, Roberta (December 1993). "Images of Mathematics Held by University Teachers of Mathematical Sciences". Educational Studies in Mathematics. 25 (4): 375–85. doi:10.1007/BF01273907. JSTOR 3482762. S2CID 122351146.
- ^ Tobies, Renate; Neunzert, Helmut (2012). Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry. Springer. p. 9. ISBN 978-3-0348-0229-1. Retrieved June 20, 2015.
[I]t is first necessary to ask what is meant by mathematics in general. Illustrious scholars have debated this matter until they were blue in the face, and yet no consensus has been reached about whether mathematics is a natural science, a branch of the humanities, or an art form.
- ^ Ziegler, Günter M.; Loos, Andreas (November 2, 2017). Kaiser, G. (ed.). "What is Mathematics?" and why we should ask, where one should experience and learn that, and how to teach it. Proceedings of the 13th International Congress on Mathematical Education. ICME-13 Monographs. Springer. pp. 63–77. doi:10.1007/978-3-319-62597-3_5. ISBN 978-3-319-62596-6. (Sections "What is Mathematics?" and "What is Mathematics, Really?")
- ^ Mura 1993, pp. 379, 381.
- ^ Brown & Porter 1995, p. 326.
- ^ Strauss, Danie (2011). "Defining mathematics". Acta Academica. 43 (4): 1–28. Retrieved November 25, 2022.
- ^ Franklin, James (2009). Philosophy of Mathematics. Elsevier. pp. 104–106. ISBN 978-0-08-093058-9. Retrieved June 20, 2015.
- ^ Cajori, Florian (1893). A History of Mathematics. American Mathematical Society (1991 reprint). pp. 285–286. ISBN 978-0-8218-2102-2. Retrieved June 20, 2015.
{{cite book}}: ISBN / Date incompatibility (help) - ^ Devlin 2018, p. 3.
- ^ Saunders Maclane (1986). Mathematics, form and function. Springer., page 409
- ^ Brown, Ronald; Porter, Timothy (1995). "The Methodology of Mathematics". The Mathematical Gazette. 79 (485): 321–334. doi:10.2307/3618304. JSTOR 3618304. S2CID 178923299. Archived from the original on March 23, 2023. Retrieved November 25, 2022.
- ^ Hamami, Yacin (June 2022). "Mathematical Rigor and Proof" (PDF). The Review of Symbolic Logic. 15 (2): 409–449. doi:10.1017/S1755020319000443. S2CID 209980693. Archived (PDF) from the original on December 5, 2022. Retrieved November 21, 2022.
- ^ Peterson 1988, p. 4: "A few complain that the computer program can't be verified properly." (in reference to the Haken–Appel proof of the Four Color Theorem)
- ^ Perminov, V. Ya. (1988). "On the Reliability of Mathematical Proofs". Philosophy of Mathematics. 42 (167 (4)). Revue Internationale de Philosophie: 500–508.
- ^ Davis, Jon D.; McDuffie, Amy Roth; Drake, Corey; Seiwell, Amanda L. (2019). "Teachers' perceptions of the official curriculum: Problem solving and rigor". International Journal of Educational Research. 93: 91–100. doi:10.1016/j.ijer.2018.10.002. S2CID 149753721.
- ^ Endsley, Kezia (2021). Mathematicians and Statisticians: A Practical Career Guide. Practical Career Guides. Rowman & Littlefield. pp. 1–3. ISBN 978-1-5381-4517-3. Retrieved November 29, 2022.
- ^ Robson, Eleanor (2009). "Mathematics education in an Old Babylonian scribal school". In Robson, Eleanor; Stedall, Jacqueline (eds.). The Oxford Handbook of the History of Mathematics. OUP Oxford. ISBN 978-0-19-921312-2. Retrieved November 24, 2022.
- ^ Bernard, Alain; Proust, Christine; Ross, Micah (2014). "Mathematics Education in Antiquity". In Karp, A.; Schubring, G. (eds.). Handbook on the History of Mathematics Education. New York: Springer. pp. 27–53. doi:10.1007/978-1-4614-9155-2_3. ISBN 978-1-4614-9154-5.
- ^ Dudley, Underwood (April 2002). "The World's First Mathematics Textbook". Math Horizons. 9 (4). Taylor & Francis, Ltd.: 8–11. doi:10.1080/10724117.2002.11975154. JSTOR 25678363. S2CID 126067145.
- ^ Subramarian, F. Indian pedagogy and problem solving in ancient Thamizhakam (PDF). History and Pedagogy of Mathematics conference, July 16–20, 2012. Archived (PDF) from the original on November 28, 2022. Retrieved November 29, 2022.
- ^ Siu, Man Keung (2004). "Official Curriculum in Mathematics in Ancient China: How did Candidates Study for the Examination?". How Chinese Learn Mathematics (PDF). Series on Mathematics Education. Vol. 1. pp. 157–185. doi:10.1142/9789812562241_0006. ISBN 978-981-256-014-8. Retrieved November 26, 2022.
- ^ Jones, Phillip S. (1967). "The History of Mathematical Education". The American Mathematical Monthly. 74 (1). Taylor & Francis, Ltd.: 38–55. doi:10.2307/2314867. JSTOR 2314867.
- ^ Schubring, Gert; Furinghetti, Fulvia; Siu, Man Keung (August 2012). "Introduction: the history of mathematics teaching. Indicators for modernization processes in societies". ZDM Mathematics Education. 44 (4): 457–459. doi:10.1007/s11858-012-0445-7. S2CID 145507519.
- ^ von Davier, Matthias; Foy, Pierre; Martin, Michael O.; Mullis, Ina V.S. (2020). "Examining eTIMSS Country Differences Between eTIMSS Data and Bridge Data: A Look at Country-Level Mode of Administration Effects". TIMSS 2019 International Results in Mathematics and Science (PDF). TIMSS & PIRLS International Study Center, Lynch School of Education and Human Development and International Association for the Evaluation of Educational Achievement. p. 13.1. ISBN 978-1-889938-54-7. Archived (PDF) from the original on November 29, 2022. Retrieved November 29, 2022.
- ^ Rowan-Kenyon, Heather T.; Swan, Amy K.; Creager, Marie F. (March 2012). "Social Cognitive Factors, Support, and Engagement: Early Adolescents' Math Interests as Precursors to Choice of Career" (PDF). The Career Development Quarterly. 60 (1): 2–15. doi:10.1002/j.2161-0045.2012.00001.x. Archived (PDF) from the original on November 22, 2023. Retrieved November 29, 2022.
- ^ Luttenberger, Silke; Wimmer, Sigrid; Paechter, Manuela (2018). "Spotlight on math anxiety". Psychology Research and Behavior Management. 11: 311–322. doi:10.2147/PRBM.S141421. PMC 6087017. PMID 30123014.
- ^ Yaftian, Narges (June 2, 2015). "The Outlook of the Mathematicians' Creative Processes". Procedia – Social and Behavioral Sciences. 191: 2519–2525. doi:10.1016/j.sbspro.2015.04.617.
- ^ Nadjafikhah, Mehdi; Yaftian, Narges (October 10, 2013). "The Frontage of Creativity and Mathematical Creativity". Procedia – Social and Behavioral Sciences. 90: 344–350. doi:10.1016/j.sbspro.2013.07.101.
- ^ van der Poorten, A. (1979). "A proof that Euler missed... Apéry's Proof of the irrationality of ζ(3)" (PDF). The Mathematical Intelligencer. 1 (4): 195–203. doi:10.1007/BF03028234. S2CID 121589323. Archived (PDF) from the original on September 6, 2015. Retrieved November 22, 2022.
- ^ Petkovi, Miodrag (September 2, 2009). Famous Puzzles of Great Mathematicians. American Mathematical Society. pp. xiii–xiv. ISBN 978-0-8218-4814-2. Retrieved November 25, 2022.
- ^ Hardy, G. H. (1940). A Mathematician's Apology. Cambridge University Press. ISBN 978-0-521-42706-7. Retrieved November 22, 2022.
{{cite book}}: ISBN / Date incompatibility (help) See also A Mathematician's Apology. - ^ Alon, Noga; Goldston, Dan; Sárközy, András; Szabados, József; Tenenbaum, Gérald; Garcia, Stephan Ramon; Shoemaker, Amy L. (March 2015). Alladi, Krishnaswami; Krantz, Steven G. (eds.). "Reflections on Paul Erdős on His Birth Centenary, Part II". Notices of the American Mathematical Society. 62 (3): 226–247. doi:10.1090/noti1223.
- ^ See, for example Bertrand Russell's statement "Mathematics, rightly viewed, possesses not only truth, but supreme beauty ..." in his History of Western Philosophy. 1919. p. 60.
- ^ Cazden, Norman (October 1959). "Musical intervals and simple number ratios". Journal of Research in Music Education. 7 (2): 197–220. doi:10.1177/002242945900700205. JSTOR 3344215. S2CID 220636812.
- ^ Budden, F. J. (October 1967). "Modern mathematics and music". The Mathematical Gazette. 51 (377). Cambridge University Press ({CUP}): 204–215. doi:10.2307/3613237. JSTOR 3613237. S2CID 126119711.
- ^ Enquist, Magnus; Arak, Anthony (November 1994). "Symmetry, beauty and evolution". Nature. 372 (6502): 169–172. Bibcode:1994Natur.372..169E. doi:10.1038/372169a0. ISSN 1476-4687. PMID 7969448. S2CID 4310147. Archived from the original on December 28, 2022. Retrieved December 29, 2022.
- ^ Hestenes, David (1999). "Symmetry Groups" (PDF).
- ^ Bender, Sara (September 2020). "The Rorschach Test". In Carducci, Bernardo J.; Nave, Christopher S.; Mio, Jeffrey S.; Riggio, Ronald E. (eds.). The Wiley Encyclopedia of Personality and Individual Differences: Measurement and Assessment. Wiley. pp. 367–376. doi:10.1002/9781119547167.ch131. ISBN 978-1-119-05751-2.
- ^ Weyl, Hermann (2015). Symmetry. Princeton Science Library. Vol. 47. Princeton University Press. p. 4. ISBN 978-1-4008-7434-7.
- ^ "Lecture 8: Translation Symmetry | Physics III: Vibrations and Waves | Physics". MIT OpenCourseWare.
- ^ Bradley, Larry (2010). "Fractals – Chaos & Fractals". stsci.edu. Archived from the original on March 7, 2023. Retrieved December 29, 2022.
- ^ "Self-similarity". math.bu.edu. Archived from the original on March 2, 2023. Retrieved December 29, 2022.
- ^ Kissane, Barry (July 2009). Popular mathematics. 22nd Biennial Conference of The Australian Association of Mathematics Teachers. Fremantle, Western Australia: Australian Association of Mathematics Teachers. pp. 125–126. Archived from the original on March 7, 2023. Retrieved December 29, 2022.
- ^ Steen, L. A. (2012). Mathematics Today Twelve Informal Essays. Springer Science & Business Media. p. 2. ISBN 978-1-4613-9435-8. Retrieved January 3, 2023.
- ^ Pitici, Mircea (2017). The Best Writing on Mathematics 2016. Princeton University Press. ISBN 978-1-4008-8560-2. Retrieved January 3, 2023.
- ^ Monastyrsky 2001, p. 1: "The Fields Medal is now indisputably the best known and most influential award in mathematics."
- ^ Riehm 2002, pp. 778–782.
- ^ "Fields Medal | International Mathematical Union (IMU)". www.mathunion.org. Archived from the original on December 26, 2018. Retrieved February 21, 2022.
- ^ a b "Fields Medal". Maths History. Archived from the original on March 22, 2019. Retrieved February 21, 2022.
- ^ "Honours/Prizes Index". MacTutor History of Mathematics Archive. Archived from the original on December 17, 2021. Retrieved February 20, 2023.
- ^ "About the Abel Prize". The Abel Prize. Archived from the original on April 14, 2022. Retrieved January 23, 2022.
- ^ "Abel Prize | mathematics award". Encyclopedia Britannica. Archived from the original on January 26, 2020. Retrieved January 23, 2022.
- ^ "Chern Medal Award" (PDF). mathunion.org. June 1, 2009. Archived (PDF) from the original on June 17, 2009. Retrieved February 21, 2022.
- ^ "Chern Medal Award". International Mathematical Union (IMU). Archived from the original on August 25, 2010. Retrieved January 23, 2022.
- ^ "The Leroy P Steele Prize of the AMS". School of Mathematics and Statistics, University of St Andrews, Scotland. Archived from the original on November 17, 2022. Retrieved November 17, 2022.
- ^ Chern, S. S.; Hirzebruch, F. (September 2000). Wolf Prize in Mathematics. doi:10.1142/4149. ISBN 978-981-02-3945-9. Archived from the original on February 21, 2022. Retrieved February 21, 2022.
- ^ "The Wolf Prize". Wolf Foundation. Archived from the original on January 12, 2020. Retrieved January 23, 2022.
- ^ a b "Hilbert's Problems: 23 and Math". Simons Foundation. May 6, 2020. Archived from the original on January 23, 2022. Retrieved January 23, 2022.
- ^ Feferman, Solomon (1998). "Deciding the undecidable: Wrestling with Hilbert's problems" (PDF). In the Light of Logic. Logic and Computation in Philosophy series. Oxford University Press. pp. 3–27. ISBN 978-0-19-508030-8. Retrieved November 29, 2022.
- ^ "The Millennium Prize Problems". Clay Mathematics Institute. Archived from the original on July 3, 2015. Retrieved January 23, 2022.
- ^ "Millennium Problems". Clay Mathematics Institute. Archived from the original on December 20, 2018. Retrieved January 23, 2022.
Other sources
[edit]- Bouleau, Nicolas (1999). Philosophie des mathématiques et de la modélisation: Du chercheur à l'ingénieur. L'Harmattan. ISBN 978-2-7384-8125-2.
- Boyer, Carl Benjamin (1991). A History of Mathematics (2nd ed.). New York: Wiley. ISBN 978-0-471-54397-8.
- Cresswell, Julia (2021). Oxford Dictionary of Word Origins (3 ed.). Oxford University Press. ISBN 978-0-19-886875-0.
- Devlin, Keith (2018). Sets, Functions, and Logic: An Introduction to Abstract Mathematics (3 ed.). CRC Press. ISBN 978-1-4822-8602-1. Archived from the original on October 7, 2024. Retrieved October 4, 2024.
- Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN 978-0-03-029558-4.
- Kleiner, Israel (2007). Kleiner, Israel (ed.). A History of Abstract Algebra. Springer Science & Business Media. doi:10.1007/978-0-8176-4685-1. ISBN 978-0-8176-4684-4. LCCN 2007932362. OCLC 76935733. S2CID 117392219. Retrieved February 8, 2024.
- Kline, Morris (1990). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. ISBN 978-0-19-506135-2.
- Monastyrsky, Michael (2001). "Some Trends in Modern Mathematics and the Fields Medal" (PDF). CMS – Notes – de la SMC. 33 (2–3). Canadian Mathematical Society. Archived (PDF) from the original on August 13, 2006. Retrieved July 28, 2006.
- Peirce, Benjamin (1881). Peirce, Charles Sanders (ed.). "Linear associative algebra". American Journal of Mathematics. 4 (1–4) (Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C.S. Peirce, of the 1872 lithograph ed.): 97–229. doi:10.2307/2369153. hdl:2027/hvd.32044030622997. JSTOR 2369153. Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed. Google Eprint and as an extract, D. Van Nostrand, 1882, Google Eprint. Retrieved November 17, 2020..
- Peterson, Ivars (1988). The Mathematical Tourist: Snapshots of Modern Mathematics. W. H. Freeman and Company. ISBN 0-7167-1953-3. LCCN 87033078. OCLC 17202382.
- Popper, Karl R. (1995). "On knowledge". In Search of a Better World: Lectures and Essays from Thirty Years. New York: Routledge. Bibcode:1992sbwl.book.....P. ISBN 978-0-415-13548-1.
- Riehm, Carl (August 2002). "The Early History of the Fields Medal" (PDF). Notices of the AMS. 49 (7): 778–782. Archived (PDF) from the original on October 26, 2006. Retrieved October 2, 2006.
- Sevryuk, Mikhail B. (January 2006). "Book Reviews" (PDF). Bulletin of the American Mathematical Society. 43 (1): 101–109. doi:10.1090/S0273-0979-05-01069-4. Archived (PDF) from the original on July 23, 2006. Retrieved June 24, 2006.
- Whittle, Peter (1994). "Almost home". In Kelly, F.P. (ed.). Probability, statistics and optimisation: A Tribute to Peter Whittle (previously "A realised path: The Cambridge Statistical Laboratory up to 1993 (revised 2002)" ed.). Chichester: John Wiley. pp. 1–28. ISBN 978-0-471-94829-2. Archived from the original on December 19, 2013.
Further reading
[edit]- Benson, Donald C. (1999). The Moment of Proof: Mathematical Epiphanies. Oxford University Press. ISBN 978-0-19-513919-8.
- Davis, Philip J.; Hersh, Reuben (1999). The Mathematical Experience (Reprint ed.). Boston; New York: Mariner Books. ISBN 978-0-395-92968-1. Available online (registration required).
- Courant, Richard; Robbins, Herbert (1996). What Is Mathematics?: An Elementary Approach to Ideas and Methods (2nd ed.). New York: Oxford University Press. ISBN 978-0-19-510519-3.
- Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W.W. Norton & Company. ISBN 978-0-393-04002-9.
- Hazewinkel, Michiel, ed. (2000). Encyclopaedia of Mathematics. Kluwer Academic Publishers. – A translated and expanded version of a Soviet mathematics encyclopedia, in ten volumes. Also in paperback and on CD-ROM, and online. Archived December 20, 2012, at archive.today.
- Hodgkin, Luke Howard (2005). A History of Mathematics: From Mesopotamia to Modernity. Oxford University Press. ISBN 978-0-19-152383-0.
- Jourdain, Philip E. B. (2003). "The Nature of Mathematics". In James R. Newman (ed.). The World of Mathematics. Dover Publications. ISBN 978-0-486-43268-7.
- Pappas, Theoni (1986). The Joy Of Mathematics. San Carlos, California: Wide World Publishing. ISBN 978-0-933174-65-8.
- Waltershausen, Wolfgang Sartorius von (1965) [1856]. Gauss zum Gedächtniss. Sändig Reprint Verlag H. R. Wohlwend. ISBN 978-3-253-01702-5.
Mathematics
View on GrokipediaEtymology and definitions
Etymology
The word mathematics derives from the Ancient Greek μάθημα (máthēma), meaning "that which is learned," "learning," "study," or "science."[10][11] In ancient Greek usage, the plural τὰ μαθήματα (ta mathēmata) referred to "the things learned" or "the mathematical sciences," encompassing arithmetic, geometry, astronomy, and harmonics (music theory), as these were grouped among the sciences concerned with number, magnitude, and proportion.[12] The term passed into Latin as mathematica (or mathematicae in plural), retaining a similar broad sense. From Latin it entered Old French as mathematique and then Middle English, appearing as mathematics in the late 16th century, initially and predominantly in plural form to reflect the Greek and Latin plural construction.[13] The related adjective mathematical derives from Latin mathematicus, itself from Greek mathematikos ("pertaining to learning" or "mathematical"). The modern narrow sense of mathematics as the study of numbers, quantities, structures, space, and change developed gradually, especially from the Renaissance onward, distinguishing it from the wider ancient inclusion of astronomy and music among the "mathematical" disciplines.[14]Definitions
Mathematics is commonly defined as the study of quantity, structure, space, and change, developed through abstraction and logical reasoning from practices such as counting, measuring, and describing shapes.[15] This characterization encompasses core areas ranging from arithmetic and algebra to geometry and analysis.[16] Alternative descriptions emphasize mathematics as the study of abstract patterns, structures, and relationships, highlighting its focus on logical connections and quantitative aspects.[17][18] Prominent mathematicians have offered distinct perspectives on its essential nature. G. H. Hardy stressed the aesthetic dimension, asserting that mathematical patterns must possess beauty comparable to those created by painters or poets, and that "beauty is the first test: there is no permanent place in this world for ugly mathematics."[19] In the early 20th century, foundational debates crystallized around three major schools of thought in the philosophy of mathematics. Logicism sought to reduce all mathematical concepts and truths to pure logic. Intuitionism viewed mathematics as fundamentally a mental activity of construction, rejecting non-constructive proofs and the independent existence of mathematical objects. Formalism, advanced by David Hilbert, treated mathematics as the manipulation of meaningless symbols according to explicit rules, with consistency serving as the key criterion for validity—Hilbert held that consistency suffices for existence within formal systems.[20][21]Pure versus applied mathematics
Pure mathematics is the study of mathematical concepts, structures, and theories for their own sake, driven by intellectual curiosity, aesthetic appeal, and the pursuit of abstract truth rather than immediate practical utility. It emphasizes rigorous proof, logical deduction, and the exploration of general properties of mathematical objects, often without concern for real-world applications at the time of discovery. Examples include areas like number theory, topology, and abstract algebra, where the primary goal is to understand fundamental mathematical principles.[6][7] Applied mathematics, in contrast, develops and employs mathematical methods to solve problems arising in other disciplines, such as physics, engineering, economics, computer science, biology, and finance. It focuses on constructing models, deriving solutions, and using computational or analytical techniques to address concrete, often real-world questions. Applied mathematics frequently involves approximations, numerical methods, optimization, and data analysis tailored to practical needs.[8][9] The boundary between pure and applied mathematics is fluid and not always sharply defined. Advances in pure mathematics frequently find unexpected and profound applications in other fields, often long after their initial development. Conversely, applied problems can inspire new pure mathematical research and lead to the creation of novel abstract theories. This interplay demonstrates the deep unity of mathematics, where abstract ideas motivated by internal logic can ultimately prove essential to understanding and advancing knowledge in the natural and social sciences.[22][23]History
Prehistoric and ancient mathematics
The earliest traces of mathematical activity appear in prehistoric times through artifacts demonstrating basic counting and recording of quantities, such as notched bones used for tallying, though systematic mathematics developed with the rise of ancient civilizations. In ancient Egypt, mathematics served practical purposes like land measurement, construction, and taxation. The Rhind Mathematical Papyrus, copied around 1650 BCE by scribe Ahmes from an older text, is a primary source documenting these techniques. It contains 84 problems involving arithmetic operations, unit fractions (expressing fractions as sums of distinct unit fractions), geometry for areas and volumes, and linear equations. Examples include calculating the area of circles using an approximation of π as (16/9)^2 and solving problems related to pyramid volumes.[24][25] The Egyptians employed a decimal system with hieroglyphic numerals and methods for multiplication and division based on repeated doubling and addition. Babylonian mathematics, flourishing from the third millennium BCE, utilized a sexagesimal (base-60) positional numeral system that supported fractional and large-number calculations more flexibly than many contemporaries. Clay tablets preserve multiplication tables, reciprocal tables, and algorithms for square and cube roots. A remarkable example is Plimpton 322, a tablet dated to approximately 1800 BCE, listing Pythagorean triples—pairs of numbers satisfying the relation corresponding to right-triangle side lengths—demonstrating practical knowledge of such relations in surveying or construction.[26] The sexagesimal system's legacy persists in modern time (60 seconds per minute, 60 minutes per hour) and angular measurement. In ancient India, the Sulba Sutras (c. 800–200 BCE), part of Vedic literature, focused on geometric constructions for ritual altars. These texts include rules equivalent to the Pythagorean theorem for right triangles and accurate approximations for √2 (such as 1 + 1/3 + 1/(3×4) - 1/(3×4×34)), as well as constructions transforming rectangles to squares.[27] Ancient Chinese mathematics developed an early decimal positional system using counting rods on boards, enabling addition, subtraction, multiplication, and division. Evidence includes sophisticated decimal multiplication tables from around 310 BCE, and the system supported practical computations in astronomy and administration.[28][29]Classical antiquity
Classical antiquity saw the emergence of mathematics as a deductive discipline in ancient Greece and the Hellenistic world, roughly from the 6th century BCE to the 3rd century CE. Greek mathematicians shifted from practical calculation and empirical observation to rigorous proof based on axioms and logical deduction, establishing a foundation that distinguished mathematics as an abstract science. Thales of Miletus (c. 624–546 BCE) is credited with the earliest known deductive proofs in geometry, demonstrating theorems such as the fact that the diameter divides a circle into two equal semicircles and that vertical angles are equal. The Pythagorean school, led by Pythagoras (c. 570–495 BCE), further developed geometry and number theory, with the famous theorem stating that in a right triangle the square of the hypotenuse equals the sum of the squares of the other two sides. Around 300 BCE, Euclid compiled the Elements, a systematic treatise in 13 books that organized plane and solid geometry, number theory, and proportions into a deductive structure beginning from five postulates, five common notions, and definitions. The work's axiomatic approach, with every proposition proved from prior results, became the paradigm for mathematical reasoning. Archimedes (c. 287–212 BCE) employed the method of exhaustion to rigorously determine areas and volumes, such as the area of the circle and the surface area and volume of the sphere, by approximating them with inscribed and circumscribed polygons and passing to the limit. Apollonius of Perga (c. 262–190 BCE) produced the definitive study of conic sections in his eight-book Conics, defining the ellipse, parabola, and hyperbola geometrically and deriving their properties through deduction. Greek number theory focused on properties of integers, including perfect numbers, amicable pairs, and primes, with Euclid proving that there are infinitely many primes and developing the algorithm for the greatest common divisor. Early algebraic techniques emerged in the Hellenistic period, particularly in solving determinate and indeterminate equations, as later exemplified in the work of Diophantus (c. 250 CE).Medieval and Islamic mathematics
During the Islamic Golden Age, roughly spanning the 8th to the 13th centuries, mathematics flourished in the Islamic world, with scholars translating and preserving ancient Greek mathematical texts into Arabic, thereby safeguarding works by Euclid, Archimedes, Apollonius, and others for later generations.[30] These translation efforts, centered in institutions such as the House of Wisdom in Baghdad, enabled Islamic mathematicians to build upon Greek geometry and number theory while integrating concepts from Indian mathematics.[30] A major contribution was the adoption and dissemination of the Hindu-Arabic numeral system, including the use of zero and positional notation, which replaced Roman numerals in many calculations and facilitated advanced arithmetic.[30] Muhammad ibn Musa al-Khwarizmi (c. 780–850) played a central role in this process through his treatise on Indian calculation methods, which introduced these numerals to the Islamic world and, later, to Europe.[30] His name also gave rise to the term "algorithm" due to the Latinized form of his name and the systematic procedures he described.[30] Al-Khwarizmi's most influential work was Al-Kitab al-mukhtasar fi hisab al-jabr wa'l-muqabala (The Compendious Book on Calculation by Completion and Balancing), which established algebra as a distinct discipline focused on solving linear and quadratic equations through systematic methods of balancing and completion.[30] This text classified quadratic equations and provided both arithmetic and geometric solutions, laying foundational principles for the field.[30] Trigonometric advances progressed significantly, with scholars refining sine tables and applying trigonometry to astronomy and spherical geometry.[30] Nasir al-Din al-Tusi (1201–1274), a Persian polymath, advanced trigonometry as an independent mathematical subject, producing accurate sine tables and developing spherical trigonometric identities that surpassed earlier work.[31] [30] Omar Khayyam (1048–1131) made notable contributions to algebra by solving cubic equations geometrically through intersections of conic sections, combining algebraic techniques with Euclidean geometry and approximation methods.[30] He also explored the parallel postulate in ways that anticipated later non-Euclidean developments.[32] Nasir al-Din al-Tusi further contributed with the Tusi couple, a geometric construction that produced straight-line motion from circular components, influencing planetary models and mathematical mechanics.[32] These achievements in algebra, arithmetic, and trigonometry, alongside the preservation of classical knowledge, formed a bridge between ancient mathematics and later European developments.[30]Renaissance to 18th century
The Renaissance in Europe, beginning in the 14th century and peaking in the 15th and 16th centuries, marked a revival of classical Greek mathematical knowledge through the translation of Arabic and Byzantine texts, combined with new innovations driven by practical needs in art, commerce, navigation, and astronomy.[33] One major development was the invention of linear perspective in art and architecture. Filippo Brunelleschi demonstrated its principles around 1415 through experiments with mirrors and drawings, enabling realistic representation of three-dimensional space on a two-dimensional surface. Leon Battista Alberti systematized these ideas in his 1435 treatise Della Pittura (On Painting), providing geometric rules for perspective construction.[33] In the 16th century, algebra advanced significantly with the solution of cubic equations by Scipione del Ferro, Niccolò Tartaglia, and Gerolamo Cardano, culminating in Cardano's publication Ars Magna (1545). Rafael Bombelli extended this work in his Algebra (1572) by introducing rules for operations involving square roots of negative numbers—early steps toward complex numbers—to resolve irreducible cubics. John Napier introduced logarithms in his 1614 work Mirifici Logarithmorum Canonis Descriptio, transforming tedious multiplications and divisions into simpler additions and subtractions, which proved invaluable for astronomical and navigational computations. René Descartes established analytic geometry in La Géométrie (1637), an appendix to his Discourse on Method. By assigning coordinates to points and expressing geometric curves through algebraic equations, he unified algebra and geometry, enabling the algebraic solution of geometric problems. Blaise Pascal and Pierre de Fermat founded probability theory through their 1654 correspondence on the "problem of points" in games of chance, developing concepts of expected value and combinatorial methods that formed the basis of modern probability. In the late 17th century, Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus (the basic ideas and notation are detailed in the Analysis section). Newton formulated his method of fluxions in the 1660s and applied it in Philosophiæ Naturalis Principia Mathematica (1687), while Leibniz published his differential and integral calculus in papers from 1684 to 1686. The 18th century was dominated by Leonhard Euler, whose vast output touched nearly every area of mathematics. He introduced influential notations including e for the base of natural logarithms, i for the square root of -1, f(x) for function notation, and Σ for summation. Euler advanced infinite series, complex analysis (notably Euler's formula e^{i\pi} + 1 = 0), number theory, differential equations, and graph theory with his 1736 solution to the Seven Bridges of Königsberg problem.19th and 20th centuries
The 19th century witnessed a profound shift toward rigor and abstraction in mathematics. The foundations of calculus, long accepted on intuitive grounds, were placed on a firmer footing through the work of Augustin-Louis Cauchy and Karl Weierstrass. Cauchy, in his 1821 Cours d'analyse, provided rigorous definitions of limits and continuity, reducing reliance on infinitesimals. Weierstrass, in the 1860s and 1870s, introduced the epsilon-delta definition of limits and continuity, precise definitions of the real numbers, and uniform convergence, resolving issues in earlier analysis. Simultaneously, the discovery of non-Euclidean geometries fundamentally altered understanding of space. Independently, Nikolai Lobachevsky (1829) and János Bolyai (1832) constructed hyperbolic geometries that satisfied all of Euclid's axioms except the parallel postulate, showing that the postulate was independent. Carl Friedrich Gauss had developed similar ideas privately earlier, while Bernhard Riemann's 1854 habilitation lecture introduced elliptic geometry and the concept of manifolds with intrinsic curvature, laying groundwork for later differential geometry. These developments demonstrated that geometry was not uniquely determined by a priori intuition, opening the door to abstract structural approaches. Algebra saw the emergence of group theory, stemming from Évariste Galois's work in the 1830s on the solvability of polynomial equations by radicals, which introduced the idea of groups of permutations. Arthur Cayley formalized the abstract notion of a group in 1854, and the subject expanded rapidly, with contributions from Camille Jordan and others, establishing groups as fundamental structures. Georg Cantor founded set theory in the 1870s, developing the theory of infinite sets, transfinite cardinals, and ordinals. His demonstration that the real numbers are uncountable (1874) and the formulation of the continuum hypothesis marked a radical expansion of mathematical objects, though it also generated paradoxes that prompted foundational crises. In the 20th century, these trends intensified. Kurt Gödel's incompleteness theorems (1931) proved that any consistent formal system powerful enough to describe arithmetic is either incomplete (containing true but unprovable statements) or inconsistent, shattering David Hilbert's program for a complete and consistent axiomatization of mathematics. The Bourbaki group, active from 1939, sought to rebuild mathematics on rigorous set-theoretic foundations, producing the multi-volume Éléments de mathématique that emphasized abstract structures (such as algebraic structures, topology, and integration) over specific examples, influencing mathematical presentation and education for decades. The advent of electronic computers enabled new forms of proof. The four color theorem, stating that four colors suffice to color any planar map so no adjacent regions share a color, was proved in 1976 by Kenneth Appel and Wolfgang Haken using computer verification of an extensive case analysis, marking the first major theorem established with essential machine assistance. Such methods expanded further in the late 20th century, though they raised philosophical questions about the nature of proof.21st-century developments
The 21st century has seen major breakthroughs in pure mathematics, alongside the rapid emergence of computational and interdisciplinary methods that are reshaping research. One landmark achievement was Grigori Perelman's proof of the Poincaré conjecture, posted in three preprints in 2002–2003 using Ricci flow with surgery to classify three-dimensional manifolds. This resolved one of the seven Millennium Prize Problems posed by the Clay Mathematics Institute.[34][35] The Langlands program, a far-reaching framework connecting number theory, geometry, and representation theory, has advanced significantly. Notable developments include the 2024 proof of the geometric Langlands conjecture by a team of nine mathematicians, establishing a key pillar of the program.[36][37] New areas have gained prominence. Tropical geometry, which replaces classical algebraic operations with min-plus algebra to yield combinatorial analogs of geometric objects, has undergone rapid development since the early 2000s and found applications in algebraic geometry and beyond.[38] Homotopy type theory, pioneered by Vladimir Voevodsky, integrates homotopy theory with dependent type theory to provide a foundation for mathematics that supports computational formalization and univalent foundations.[39] Machine learning has increasingly contributed to mathematical discovery. Collaborations involving DeepMind have used neural networks to identify new patterns and conjectures in areas such as knot theory and representation theory, demonstrating AI's potential as a research partner.[40][37] These developments reflect a broader trend toward hybrid approaches combining rigorous proof with computational tools and novel perspectives.Foundations
Mathematical logic
Mathematical logic is the study of formal systems of logic, their expressive power, proof procedures, and limitations, providing the rigorous foundation for reasoning in mathematics and computer science. Propositional logic, also known as sentential logic, formalizes reasoning using propositions combined with logical connectives including negation (¬), conjunction (∧), disjunction (∨), implication (→), and equivalence (↔). Its semantics are defined via truth tables, which assign truth values to compound formulas based on the values of atomic propositions. Propositional logic is decidable, as any formula can be mechanically checked for validity or satisfiability using truth tables or efficient algorithms like the Davis–Putnam–Logemann–Loveland procedure. Predicate logic, or first-order logic, extends propositional logic by including variables, quantifiers (universal ∀ and existential ∃), and predicates that express properties and relations among objects. It allows statements such as ∀x (P(x) → Q(x)), expressing "for all x, if P holds for x then Q holds for x." The syntax includes terms, atomic formulas, and recursive formation of complex formulas using connectives and quantifiers. First-order logic is the standard logic for most mathematical theories due to its balance of expressive power and manageability. Kurt Gödel's completeness theorem (1930) establishes that every logically valid sentence in first-order logic has a proof in the standard Hilbert-style axiomatization, meaning that semantic entailment coincides with syntactic provability. In contrast, Gödel's first incompleteness theorem (1931) shows that any consistent formal system capable of expressing basic arithmetic (such as Peano arithmetic) is incomplete: there exist true statements in the language of the system that cannot be proved within it. The second incompleteness theorem states that such a system cannot prove its own consistency, assuming it is consistent. These results demonstrated fundamental limitations of formal axiomatic systems. Computability theory, pioneered by Alan Turing, addresses which functions can be mechanically computed. Turing introduced the Turing machine in 1936 as an abstract model of computation consisting of an infinite tape, a read/write head, and a finite set of states with transition rules. A function is computable if there exists a Turing machine that computes it. The Church-Turing thesis posits that any effectively calculable function can be computed by a Turing machine (or equivalent models such as lambda calculus or recursive functions). Undecidable problems, such as the halting problem, show that no algorithm exists to determine whether an arbitrary Turing machine halts on a given input. Decidability concerns whether a problem has an algorithmic solution: a decision problem is decidable if there is a Turing machine that halts on all inputs and correctly outputs yes or no. Many fundamental questions in mathematics are undecidable, such as the Entscheidungsproblem posed by Hilbert, which Turing and Church independently proved undecidable in 1936. Recursion theory, closely related to computability, classifies functions into recursive (computable) and recursively enumerable sets, and studies Turing degrees measuring relative computability. Model theory investigates the relationships between formal languages and their interpretations in structures. A model of a theory is a structure (domain with interpretations of constants, functions, and relations) that satisfies all sentences of the theory. Key results include the compactness theorem, which states that a set of first-order sentences has a model if every finite subset does, and Löwenheim–Skolem theorems, which guarantee models of various cardinalities. Model theory provides tools to study algebraic structures, definability, and classification of theories. but since no Wikipedia, perhaps skip citation. Mathematical logic underpins set theory by providing the formal language in which axiomatic systems are expressed, though detailed set-theoretic axioms are treated separately.Set theory
Set theory is the branch of mathematics that studies sets, abstract collections of distinct objects considered independently of their internal structure or order. It provides a foundational framework for most of modern mathematics by allowing the definition of mathematical objects—such as numbers, functions, and spaces—as sets and by formalizing proofs in terms of set membership and operations. The standard axiomatic system for set theory is Zermelo-Fraenkel set theory with the axiom of choice (ZFC), which includes axioms for extensionality, the empty set, pairing, union, power set, infinity, separation, replacement, regularity (foundation), and the axiom of choice. ZFC avoids paradoxes like Russell's by restricting set formation and enables the rigorous construction of mathematical structures. Within ZFC, ordinal numbers are well-ordered sets used to measure the order type of well-orderings, while cardinal numbers measure the size of sets. Ordinals are transitive sets well-ordered by membership, and cardinals are initial ordinals (ordinals not equinumerous to any smaller ordinal). Infinite cardinals are denoted by alephs (), with being the cardinality of the natural numbers and subsequent alephs indexing larger infinite sizes. A central question in set theory is the continuum hypothesis (CH), which asserts that there is no set whose cardinality is strictly between that of the natural numbers and that of the real numbers, i.e., . In 1938, Kurt Gödel proved the consistency of CH (and the generalized continuum hypothesis, GCH) relative to ZFC by constructing the constructible universe , the smallest transitive inner model of ZFC containing all ordinals, in which GCH holds and every set is definable from ordinals in a hierarchical manner.[41][42] In 1963, Paul Cohen introduced the technique of forcing to prove the independence of CH from ZFC, showing that the negation of CH is also consistent with ZFC. Forcing constructs extensions of models of ZFC by adding generic sets, allowing control over cardinal arithmetic and truth of statements like CH. Together, Gödel's and Cohen's results established that CH is undecidable in ZFC: neither CH nor its negation can be proved from ZFC alone.[41] The constructible universe remains a key object in set theory, serving as the canonical inner model for many consistency results and forming the foundation for inner model theory. Forcing has since become a primary method for establishing independence and consistency results in set theory.[41]Axiomatic method
The axiomatic method is a cornerstone of modern mathematics, characterized by the development of a mathematical theory from a small set of precisely stated axioms (or postulates) and definitions, with all subsequent propositions derived through strict logical deduction. This approach ensures rigor, eliminates ambiguity, and establishes a clear hierarchy of truths within a given domain. By starting from minimal, self-evident or agreed-upon assumptions, it allows mathematicians to build complex structures while maintaining deductive certainty.[43] The earliest and most influential exemplar of the axiomatic method is Euclid's Elements (circa 300 BCE), which presented plane and solid geometry in a systematic deductive framework. Euclid began with a series of definitions (e.g., point, line, straight line), five postulates (including the parallel postulate), and five common notions (such as "things equal to the same thing are equal to each other"), from which he derived hundreds of propositions through logical inference. This structure not only organized existing geometric knowledge but also established the axiomatic method as a paradigm for rigorous proof in mathematics, influencing subsequent developments across the discipline.[44][45] In the late 19th and early 20th centuries, David Hilbert revitalized and extended the axiomatic method as part of his formalist program. Hilbert advocated for the complete formalization of all branches of mathematics through axiomatic systems, emphasizing the independence of axioms from intuitive content and focusing on their consistency and completeness. His approach sought to prove the consistency of such systems using finitary (finite, constructive) methods, thereby securing mathematics against contradictions. Although Kurt Gödel's incompleteness theorems (1931) demonstrated inherent limitations—showing that sufficiently powerful consistent axiomatic systems cannot prove their own consistency—Hilbert's program profoundly shaped modern mathematical logic, proof theory, and foundational studies.[46] More recently, category theory has provided a structural extension of the axiomatic method. Introduced by Samuel Eilenberg and Saunders Mac Lane in the 1940s, category theory shifts emphasis from the internal composition of mathematical objects to the morphisms (structure-preserving maps) between them and their compositions. It axiomatizes mathematical structures in terms of universal properties, functors, and natural transformations, enabling a highly abstract and unified treatment of relationships across diverse branches of mathematics (such as algebra, topology, and logic). This categorical perspective offers a "structural" form of axiomatization, where the focus lies on patterns of mappings and transformations rather than on the elements of the objects themselves.[47][48] The axiomatic method, in its various forms, remains fundamental to contemporary mathematics, underpinning the clarity, generality, and logical strength of the discipline.Philosophy of mathematics
The philosophy of mathematics examines fundamental questions about the nature of mathematical objects, the source of mathematical truth, and the meaning of mathematical statements. Central to the field is the debate over whether mathematical entities—such as numbers, functions, and sets—exist independently of human minds and physical reality, or whether they are human constructs, formal symbols, or fictions. Platonism, one of the most influential positions, asserts that mathematical objects exist as abstract, non-physical entities in their own right, independent of space, time, and human cognition. Proponents hold that mathematicians discover rather than invent these objects, and that mathematical truths are objective and necessary. A key argument for this view stems from Gottlob Frege, who contended that the apparent reference to abstract entities in mathematical statements provides evidence for their existence. [49] Major alternative positions include formalism, which regards mathematics as a formal system of symbols manipulated according to syntactic rules, without any commitment to the existence of mathematical objects or meaning beyond consistency within the system. Intuitionism, developed by L. E. J. Brouwer, maintains that mathematical objects are mental constructions that must be explicitly constructed to be legitimate, rejecting non-constructive existence proofs and certain classical logical principles. Logicism, advocated by Gottlob Frege and Bertrand Russell, seeks to reduce all of mathematics to pure logic, thereby grounding mathematical truth in logical truth. [50] More recent views include structuralism, which emphasizes that mathematics studies relational structures rather than individual objects, and fictionalism, which treats mathematical assertions as useful fictions that are not literally true but serve practical purposes in science and reasoning. The ongoing debate over the existence of mathematical objects reflects deep divisions between realist positions like Platonism, which affirm an independent mathematical reality, and various anti-realist alternatives, which seek to avoid ontological commitment to such entities. Gödel's incompleteness theorems have influenced this discussion by highlighting limits in formal systems, though they do not resolve the core ontological questions.Major branches of pure mathematics
Number theory
Number theory is the branch of pure mathematics primarily concerned with the properties and relationships of integers, particularly the positive integers, and related concepts such as divisibility, primes, and congruences. A central object of study is the prime numbers, which are integers greater than 1 with no positive divisors other than 1 and themselves. The distribution and properties of primes have driven much of the development in the field. The Fundamental Theorem of Arithmetic states that every positive integer greater than 1 can be expressed uniquely as a product of prime numbers, up to the order of the factors.[51][52] This unique factorization property underpins many results in number theory and related areas. Number theory also investigates Diophantine equations, which seek integer solutions to polynomial equations, and modular arithmetic, the arithmetic of integers modulo a fixed integer, which provides tools for solving such equations and analyzing divisibility. Analytic number theory uses tools from complex analysis to study the distribution of primes and other arithmetic functions. The Prime Number Theorem, proved independently by Jacques Hadamard and Charles-Jean de la Vallée Poussin in 1896, states that the number of primes less than or equal to a large number , denoted , is asymptotically .[53][54][55] This theorem is deeply connected to the Riemann zeta function, initially defined for complex numbers with real part greater than 1 as The zeta function can be analytically continued to the entire complex plane (except for a pole at ) and its non-trivial zeros are linked to the precise distribution of primes.[56][57]Algebra
Algebra is the branch of pure mathematics concerned with the study of algebraic structures such as groups, rings, and fields, emphasizing their abstract properties and relationships rather than specific numerical computations.[58] These structures generalize familiar number systems like the integers and rational numbers by focusing on operations that satisfy certain axioms, enabling the unification of diverse mathematical phenomena.[59] A group consists of a set equipped with a single binary operation that is associative, has an identity element, and for which every element has an inverse. Groups capture the essence of symmetry and are foundational to many areas of mathematics. Rings extend this idea by incorporating two operations—typically addition and multiplication—where the set forms an abelian group under addition, multiplication is associative and distributive over addition, and there is usually a multiplicative identity. Fields are commutative rings in which every nonzero element has a multiplicative inverse, providing a setting analogous to the rational, real, or complex numbers.[60][61] Galois theory links field extensions with group theory, associating to each extension a Galois group of automorphisms that fix the base field. This correspondence, particularly the fundamental theorem of Galois theory, determines whether polynomial equations are solvable by radicals through the solvability of the associated group. Emil Artin contributed significantly to its modern formulation by providing an elegant, axiomatic presentation that avoided certain arbitrary choices in earlier approaches.[62][63] Linear algebra studies vector spaces, which are abelian groups equipped with scalar multiplication from a field, and linear transformations between them. Matrices represent these transformations relative to bases, facilitating computations such as solving systems of linear equations, finding eigenvalues, and analyzing linear independence. In abstract terms, vector spaces generalize geometric notions of direction and magnitude while serving as modules over rings in broader contexts.[61] In the early 20th century, abstract algebra underwent profound development. Emmy Noether revolutionized the subject through her work on ring theory, particularly by introducing the concept of Noetherian rings (satisfying the ascending chain condition on ideals), which unified and generalized earlier results in commutative and noncommutative algebra.[64] Emil Artin advanced the theory of noncommutative rings and Artinian rings (satisfying the descending chain condition on right ideals), while also influencing the presentation of Galois theory. Together, Noether and Artin are regarded as founders of modern abstract algebra.[65]Geometry
Geometry is the branch of mathematics that studies the properties, measurements, and relationships of points, lines, angles, surfaces, and solids in space. It explores shapes and their configurations in various dimensions and types of spaces.[66] Euclidean geometry, the classical form based on the axioms presented by Euclid in his Elements (circa 300 BCE), assumes flat space where the parallel postulate holds: through a point not on a given line, exactly one parallel line can be drawn. This framework underpins much of elementary geometry and includes fundamental results such as the Pythagorean theorem, which asserts that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides: . In the early 19th century, the discovery of consistent non-Euclidean geometries challenged the universality of Euclid's parallel postulate. Hyperbolic geometry (also known as Lobachevsky-Bolyai-Gauss geometry) allows infinitely many lines through a point parallel to a given line, while elliptic geometry (Riemannian geometry) allows none. These geometries have constant negative curvature for hyperbolic and positive for elliptic spaces.[67] Differential geometry applies calculus to the study of curves, surfaces, and higher-dimensional manifolds. It introduces intrinsic properties such as Gaussian curvature, independent of embedding, and Riemannian metrics that enable the measurement of distances and angles on curved spaces. Bernhard Riemann's work on n-dimensional manifolds with variable curvature provided the foundation for modern differential geometry and later applications in physics. Algebraic geometry investigates geometric objects defined as solutions to systems of polynomial equations. In classical algebraic geometry, these objects are algebraic varieties—zero sets of polynomials in affine or projective space—studied using tools from commutative algebra, particularly polynomial rings.[68] Geometry differs from topology in its emphasis on metric and rigid structures rather than merely continuous properties.Topology
Topology is the branch of mathematics that studies properties of spaces that are preserved under continuous deformations, such as stretching, crumpling, and bending, but not tearing or gluing. These properties are qualitative rather than quantitative, distinguishing topology from geometry, which focuses on rigid measurements like distances and angles. Point-set topology, also known as general topology, provides the foundational framework for the subject. It begins with the concept of a topological space, which consists of a set X equipped with a collection of subsets called open sets that satisfy three axioms: the empty set and X itself are open; arbitrary unions of open sets are open; and finite intersections of open sets are open. Closed sets are defined as complements of open sets. Continuity of functions between topological spaces is defined topologically: a function f: X → Y is continuous if the preimage of every open set in Y is open in X. Key properties include compactness, where every open cover has a finite subcover, and connectedness, where the space cannot be expressed as the union of two disjoint nonempty open sets. Other important concepts in point-set topology include Hausdorff spaces (where distinct points have disjoint neighborhoods), bases and subbases for topologies, and separation axioms that classify spaces by how well open sets can distinguish points. Algebraic topology employs tools from abstract algebra to distinguish topological spaces and study their properties more effectively. It associates algebraic invariants to spaces that remain unchanged under homeomorphisms. Homotopy theory examines continuous deformations of maps, leading to homotopy groups that classify loops and higher-dimensional analogs up to deformation. Homology theory assigns abelian groups to spaces by considering simplicial or singular chains, with homology groups detecting "holes" of various dimensions; for example, the first homology group relates to loops that cannot be contracted. Topology intersects with other areas, such as in the study of manifolds, which are topological spaces locally homeomorphic to Euclidean space (though detailed treatment of manifolds appears in differential geometry).Analysis
Mathematical analysis is the branch of pure mathematics devoted to the rigorous study of limits and the concepts that arise from them, including continuity, differentiation, integration, and infinite series. It extends the intuitive ideas of calculus to provide a firm foundation for understanding change and accumulation in continuous settings. The field encompasses real analysis, which focuses on functions of real variables; complex analysis, which deals with functions of complex variables; and advanced extensions such as functional analysis and measure theory.[69][70] In real analysis, the concept of a limit is fundamental, describing the behavior of a function or sequence as its input approaches a particular value or infinity. A function f is continuous at a point a if the limit of f(x) as x approaches a equals f(a). Differentiation formalizes the notion of instantaneous rate of change through the derivative, defined as the limit of the difference quotient: f'(a) = lim_{h→0} [f(a+h) - f(a)] / h, when this limit exists. Integration, particularly the Riemann integral, defines the area under a curve as the limit of sums of areas of approximating rectangles. The Fundamental Theorem of Calculus establishes the deep connection between differentiation and integration, consisting of two main parts. One part states that if a function f is continuous on [a, b] and F(x) is defined as the integral from a to x of f(t) dt, then F is differentiable and F'(x) = f(x). The other part asserts that the integral from a to b of f'(x) dx equals f(b) - f(a), provided f' is integrable. These results show that integration and differentiation are inverse operations under suitable conditions.[71][72][73] Complex analysis extends these ideas to functions of a complex variable, where the requirement of complex differentiability (analyticity) imposes strong conditions, leading to powerful results such as Cauchy's integral theorem and the residue theorem, which facilitate evaluation of real integrals and have applications in many areas of mathematics and physics. Functional analysis studies vector spaces endowed with topological structures, particularly infinite-dimensional spaces such as Banach spaces (complete normed vector spaces) and Hilbert spaces (complete inner product spaces). It generalizes concepts from linear algebra and analysis to handle operators on these spaces, with key applications in differential equations, quantum mechanics, and optimization.[69] Measure theory provides a rigorous framework for generalizing the notion of length, area, and volume to abstract sets, culminating in the Lebesgue measure and Lebesgue integral. Unlike the Riemann integral, the Lebesgue integral handles a broader class of functions, including those with discontinuities on sets of measure zero, and supports powerful convergence theorems such as the dominated convergence theorem. This foundation underpins modern probability theory and advanced real analysis.[69]Discrete mathematics
Discrete mathematics is the branch of mathematics concerned with mathematical structures that are fundamentally discrete rather than continuous, dealing with countable or otherwise distinct objects such as integers, graphs, and finite sets.[74] In contrast to continuous mathematics, which addresses phenomena varying smoothly, discrete mathematics focuses on objects that appear in separate bundles or isolated values.[75][76] This field has grown in importance with the rise of computer science, serving as a foundational tool for algorithm design, computational complexity analysis, and modeling problems involving finite or countable structures.[77] Combinatorics forms a central pillar of discrete mathematics, addressing problems of counting, arrangement, and combination of discrete objects. It encompasses techniques such as permutations and combinations, the pigeonhole principle, inclusion-exclusion, and generating functions, which provide systematic ways to enumerate possibilities and solve counting problems in diverse contexts.[78] Graph theory studies graphs—structures consisting of vertices (nodes) connected by edges—modeling pairwise relationships among discrete entities. Key concepts include paths, cycles, trees, connectivity, planarity, and graph coloring, with applications ranging from network design to scheduling problems.[78][79] Algorithms in discrete mathematics involve the design and analysis of procedures for solving problems on discrete structures, often relying on recurrence relations to express the running time or space complexity of recursive processes. Recurrence relations, such as those arising in divide-and-conquer strategies, are solved using methods like substitution, generating functions, or the master theorem, enabling precise performance analysis of algorithms.[80] Discrete mathematics also provides the foundational concepts for cryptography, particularly through structures that support secure key exchange and encryption schemes resistant to classical attacks, including those based on discrete logarithmic problems and integer factorization.[81]Probability and statistics
Probability theory
Probability theory is the branch of mathematics that develops models for randomness and uncertainty using rigorous deduction. It provides the formal framework to quantify the likelihood of events, analyze random phenomena, and derive probabilistic conclusions from axioms. Probability theory serves as the theoretical foundation for statistics, which focuses on inference from data.[82] The contemporary foundations of probability theory were established by Andrey Kolmogorov in his 1933 work, where he axiomatized probability in a manner parallel to measure theory. A probability space consists of a sample space Ω, a σ-algebra \mathcal{F} of events, and a probability measure P satisfying the Kolmogorov axioms:- For every event A ∈ \mathcal{F}, P(A) ≥ 0.
- P(Ω) = 1.
- For any countable collection of pairwise disjoint events {A_i}{i=1}^∞, P(\bigcup{i=1}^∞ A_i) = \sum_{i=1}^∞ P(A_i).









